
【題目】設![]() ,函數
,函數![]()
(1)若![]() ,求出函數
,求出函數![]() 在區間上
在區間上![]() 的最大值.
的最大值.
(2)若![]() ,求出函數
,求出函數![]() 的單調區間(不必證明)
的單調區間(不必證明)
(3)若存在![]() ,使得關于
,使得關于![]() 方程
方程![]() 有三個不相等的實數根,求出實數
有三個不相等的實數根,求出實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]()
(2)遞增區間![]() 和
和![]() 遞減區間
遞減區間![]()
(3)![]()
【解析】
(1)當![]() 時,
時,![]() ,結合去絕對值解法求最值即可;
,結合去絕對值解法求最值即可;
(2)同樣是采用去絕對值解法,寫出分段函數,畫出函數大致圖像,判斷函數增減區間即可;
(3)可結合(1)(2)結果,以![]() 為分界,再結合函數圖像確定函數圖像的增減性,結合數形結合思想得出關于參數
為分界,再結合函數圖像確定函數圖像的增減性,結合數形結合思想得出關于參數![]() 的不等式,再結合對勾函數性質即可求解
的不等式,再結合對勾函數性質即可求解
(1)當![]() 時,
時,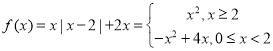 ,畫出函數圖像,如圖:
,畫出函數圖像,如圖:
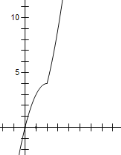
當![]() 時,函數為增函數,
時,函數為增函數,![]() ;
;
(2)當![]() 時,
時,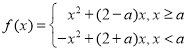 ,
,
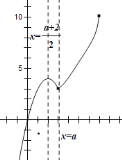
當![]() 時,函數對稱軸為
時,函數對稱軸為![]() ,所以當
,所以當![]() 時,
時,![]() 單調遞增;
單調遞增;
當![]() 時,函數對稱軸為
時,函數對稱軸為![]() ,當
,當![]() 時,函數單調遞增,當
時,函數單調遞增,當![]() 時,函數單調遞減,
時,函數單調遞減,
綜上所述,當![]() 和
和![]() 時,函數
時,函數![]() 單增,當
單增,當![]() 時,函數
時,函數![]() 單調遞減;
單調遞減;
(3)當![]() 時,
時,![]() ,函數在
,函數在![]() 時單增,
時單增,![]() ,此時分段函數對應的對稱軸在
,此時分段函數對應的對稱軸在![]() 軸右側,則
軸右側,則![]() 在
在![]() 時,
時,![]() 也時單增,不可能使得
也時單增,不可能使得
![]() 有三個不相等的實數根;
有三個不相等的實數根;
當![]() 時,
時,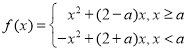 ,要使
,要使![]() 有三個不相等的實數根,即
有三個不相等的實數根,即![]() 應介于如圖所示兩虛線范圍之間,
應介于如圖所示兩虛線范圍之間,![]() ,當
,當![]() 時,
時,
![]() ,即
,即![]() ,
,
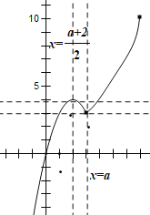
化簡得![]() ,
,![]() ,
,![]() 時取到最小值,當
時取到最小值,當![]() 時,
時,![]() 單調遞增(對勾函數性質),則
單調遞增(對勾函數性質),則![]() ,
,
故![]() ,故
,故![]()


 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】空氣質量指數AQI是一種反映和評價空氣質量的方法,AQI指數與空氣質量對應如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
如圖是某城市2018年12月全月的AQI指數變化統計圖:

根據統計圖判斷,下列結論正確的是( )
A. 整體上看,這個月的空氣質量越來越差
B. 整體上看,前半月的空氣質量好于后半個月的空氣質量
C. 從AQI數據看,前半月的方差大于后半月的方差
D. 從AQI數據看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中數學 來源: 題型:
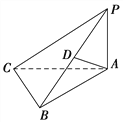
【題目】如圖所示,在三棱錐P–ABC中,PA⊥平面ABC,D是棱PB的中點,已知PA=BC=2,AB=4,CB⊥AB,則異面直線PC,AD所成角的余弦值為
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() ,動直線
,動直線![]() 過定點
過定點![]() 且交橢圓
且交橢圓![]() 于
于![]() ,
,![]() 兩點(
兩點(![]() ,
,![]() 不在
不在![]() 軸上).
軸上).
(1)若線段![]() 中點
中點![]() 的縱坐標是
的縱坐標是![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)記![]() 點關于
點關于![]() 軸的對稱點為
軸的對稱點為![]() ,若點
,若點![]() 滿足
滿足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為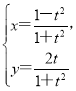 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求C的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)求C上的點到![]() 距離的最大值.
距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將四個面都為直角三角形的四面體稱為鱉臑.如圖,四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形,![]() ,
,![]() ,
,![]() 底面
底面![]() .
.
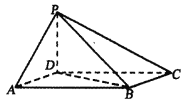
(1)求證:![]() 平面
平面![]() .試判斷四面體
.試判斷四面體![]() 是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
(2)若![]() ,求點A到平面
,求點A到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一幢高樓上安放了一塊高約10 米的 LED 廣告屏,一測量愛好者在與高樓底部同一水平線上的 C 處測得廣告屏頂端A 處的仰角為 31.80°,再向大樓前進 20 米到 D 處,測得廣告屏頂端 A 處的仰角為 37.38°(人的高度忽略不計).
(1)求大樓的高度(從地面到廣告屏頂端)(精確到 1 米);
(2)若大樓的前方是一片公園空地,空地上可以安放一些長椅,為使坐在其中一個長椅上觀看廣告屏最清晰(長 椅的高度忽略不計),長椅需安置在距大樓底部 E 處多遠?已知視角 ∠AMB( M 為觀測者的位置, B 為廣告屏 底部)越大,觀看得越清晰.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() ,以坐標原點
,以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸,直線
軸正半軸為極軸,直線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 交圓
交圓![]() 于
于![]() 兩點,
兩點,![]() 為
為![]() 中點.
中點.
(1)求點![]() 軌跡的極坐標方程;
軌跡的極坐標方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com