
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() 平面
平面![]() ,
,![]() 為
為![]() 的中點.
的中點.
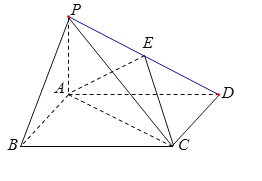
(1)證明:![]() ∥平面
∥平面![]() .
.
(2)設二面角![]() 為
為![]() ,
,![]() ,
,![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
【答案】(1)見解析(2)![]()
【解析】
(1)連結![]() 交
交![]() 于點
于點![]() ,連結
,連結![]() . 根據四邊形
. 根據四邊形![]() 為矩形,所以
為矩形,所以![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,利用三角形的中位線可得
的中點,利用三角形的中位線可得![]() ∥
∥![]() ,再利用線面平行的判定定理證明.
,再利用線面平行的判定定理證明.
(2) 根據![]() 平面
平面![]() ,四邊形
,四邊形![]() 為矩形,建立空間直角坐標系
為矩形,建立空間直角坐標系![]() .設
.設![]() ,再求得平面DAE, 平面CAE的法向量,根據二面角
,再求得平面DAE, 平面CAE的法向量,根據二面角![]() 為
為![]() ,利用
,利用![]() ,解得
,解得![]() .,然后利用錐體體積公式求解.
.,然后利用錐體體積公式求解.
(1)連結![]() 交
交![]() 于點
于點![]() ,連結
,連結![]() .
.
因為四邊形![]() 為矩形,所以
為矩形,所以![]() 為
為![]() 的中點,
的中點,
又![]() 為
為![]() 的中點,所以
的中點,所以![]() ∥
∥![]() ,
,
且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
(2) 因為![]() 平面
平面![]() ,四邊形
,四邊形![]() 為矩形,所以
為矩形,所以![]() 兩兩垂直,
兩兩垂直,
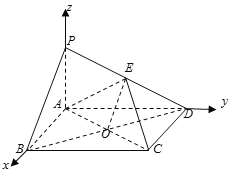
以![]() 為坐標原點,
為坐標原點,![]() 的方向為
的方向為![]() 軸的正方向,
軸的正方向,![]() 的方向為
的方向為![]() 軸的正方向,
軸的正方向,![]() 的方向為
的方向為![]() 軸的正方向,
軸的正方向,![]() 為單位長,建立空間直角坐標系
為單位長,建立空間直角坐標系![]() .
.
設![]() ,則
,則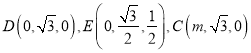 ,
,
所以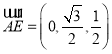 ,
,![]()
設![]() 為平面
為平面![]() 的法向量,則
的法向量,則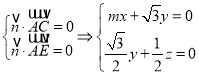 ,
,
可取![]() ,
,
又![]() 為平面
為平面![]() 的一個法向量,由題設知
的一個法向量,由題設知![]()
即![]() ,解得
,解得![]() .
.
因為![]() 為
為![]() 的中點,設
的中點,設![]() 為
為![]() 的中點,
的中點,
則![]() ∥
∥![]() ,且
,且![]() ,
,![]() ⊥面
⊥面![]() ,
,
故有三棱錐![]() 的高為
的高為![]() ,
,
三棱錐![]() 的體積
的體積![]()
所以三棱錐![]() 的體積為
的體積為![]() .
.


科目:高中數學 來源: 題型:
【題目】2013年至201 9年我國二氧化硫的年排放量(單位:萬噸)如下表,則以下結論中錯誤的是( )
![]()
A.二氧化硫排放量逐年下降
B.2018年二氧化硫減排效果最為顯著
C.2017年至2018年二氧化硫減排量比2013年至2016年二氧化硫減排量的總和大
D.2019年二氧化硫減排量比2018年二氧化硫減排量有所增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在開展學習強國的活動中,某校高三數學教師成立了黨員和非黨員兩個學習組,其中黨員學習組有4名男教師、1名女教師,非黨員學習組有2名男教師、2名女教師,高三數學組計劃從兩個學習組中隨機各選2名教師參加學校的挑戰答題比賽.
(1)求選出的4名選手中恰好有一名女教師的選派方法數;
(2)記X為選出的4名選手中女教師的人數,求X的概率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據氣象部門預報,在距離某個碼頭A南偏東45°方向的600km處的熱帶風暴中心B正以30km/h的速度向正北方向移動,距離風暴中心450km以內的地區都將受到影響,從現在起經過___小時后該碼頭A將受到熱帶風暴的影響(精確到0.01).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】支付寶和微信支付已經成為現如今最流行的電子支付方式,某市通過隨機詢問100名居民(男女居民各50名)喜歡支付寶支付還是微信支付,得到如下的![]() 列聯表:
列聯表:
支付寶支付 | 微信支付 | |
男 | 40 | 10 |
女 | 25 | 25 |
附表及公式: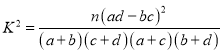 ,
,![]() .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
則下面結論正確的是( )
A.有![]() 以上的把握認為“支付方式與性別有關”
以上的把握認為“支付方式與性別有關”
B.在犯錯誤的概率超過![]() 的前提下,認為“支付方式與性別有關”
的前提下,認為“支付方式與性別有關”
C.在犯錯誤的概率不超過![]() 的前提下,認為“支付方式與性別有關”
的前提下,認為“支付方式與性別有關”
D.有![]() 以上的把握認為“支付方式與性別無關”
以上的把握認為“支付方式與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在![]() 中,兩直角邊
中,兩直角邊![]() ,
,![]() 的長分別為
的長分別為![]() 和
和![]() ,以
,以![]() 的中點
的中點![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,以
軸,以![]() 的垂直平分線為
的垂直平分線為![]() 軸建立平面直角坐標系,橢圓
軸建立平面直角坐標系,橢圓![]() 以
以![]() ,
,![]() 為焦點,且經過點
為焦點,且經過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() :
:![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 為等邊三角形,若存在,求出直線
為等邊三角形,若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com