分析 由題意設出圖象的對稱中心的坐標，列出滿足的恒等式，代入函數解析式列出方程，根據方程兩邊對應系數相等求出a和b的值．
解答 解：由題意設對稱中心的坐標為（a，b），
則有2b=f（a+x）+f（a-x）對任意x均成立，代入函數解析式得，
2b=（a+x）3-3（a+x）2-9（a+x）+（a-x）3-3（a-x）2-9（a-x）對任意x均成立，
∴a=1，
代入上面的等式解得b=-11，即對稱中心（1，-11）．
故答案為：（1，-11）．
點評 本題考查了函數圖象中心對稱的性質的應用，即函數的對稱中心的坐標是（a，b），則有2b=f（a+x）+f（a-x）對任意x均成立，由此恒等式進行求值．
科目：高中數學 來源： 題型：選擇題
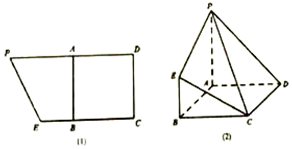已知梯形CEPD如圖（1）所示，其中PD=8，CE=6，A為線段PD的中點，四邊形ABCD為正方形，現沿AB進行折疊，使得平面PABE⊥平面ABCD，得到如圖（2）所示的幾何體．已知當點F滿足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$（0＜λ＜1）時，平面DEF⊥平面PCE，則λ的值為（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
查看答案和解析>>
科目：高中數學 來源： 題型：選擇題
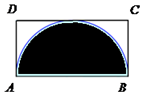若將一個質點隨機投入如圖所示的長方形ABCD中，其中AB=2，BC=1，則質點落在以AB為直徑的半圓內的概率是（ ）| A． | $\frac{π}{8}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{5}$ | D． | $\frac{π}{2}$ |
查看答案和解析>>
科目：高中數學 來源： 題型：選擇題
若二次函數f（x）的圖象與x軸有兩個異號交點，它的導函數f'（x）的圖象如圖所示，則函數f（x）圖象的頂點在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
查看答案和解析>>
科目：高中數學 來源： 題型：選擇題
| A． | sin（$-\frac{π}{18}$）＞sin（$-\frac{π}{10}$） | B． | sin250°＞sin260° | C． | tan$\frac{π}{4}$＞tan$\frac{π}{6}$ | D． | tan138°＞tan143° |
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
如圖，在圓心角為直角的扇形OAB中，分別以OA，OB為直徑作兩個半圓，設OA=1，則陰影部分的面積是$\frac{π-2}{4}$．