
【題目】函數![]() ,
,![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)答案見解析;(2)![]() .
.
【解析】
(1)求出函數![]() 的定義域為
的定義域為![]() ,求得
,求得![]() ,分
,分![]() 、
、![]() 、
、![]() 三種情況討論,分析導數的符號變化,由此可得出函數
三種情況討論,分析導數的符號變化,由此可得出函數![]() 的單調遞增區間和遞減區間;
的單調遞增區間和遞減區間;
(2)構造函數![]() ,由題意可知
,由題意可知![]() 恒成立,對實數
恒成立,對實數![]() 分
分![]() 和
和![]() 兩種情況討論,利用導數分析函數
兩種情況討論,利用導數分析函數![]() 在區間
在區間![]() 上的單調性,驗證
上的單調性,驗證![]() 是否成立,由此可得出實數
是否成立,由此可得出實數![]() 的取值范圍.
的取值范圍.
(1)函數![]() 的定義域為
的定義域為![]() ,
,![]() .
.
(i)當![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
(ii)當![]() 時,令
時,令![]() 得
得![]() .
.
若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() .
.
①當![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
②當![]() 時,
時,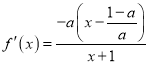 ,
,
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增;當
單調遞增;當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減;
單調遞減;
綜上,可得,當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
(2)設![]() ,
,![]() ,則
,則![]() .
.
當![]() 時,
時,![]() 單調遞增,則
單調遞增,則![]() .
.
所以,函數![]() 在
在![]() 上單調遞增,且
上單調遞增,且![]() .
.
當![]() 時,
時,![]() ,
,
于是,函數![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 恒成立,符合題意;
恒成立,符合題意;
當![]() 時,由于
時,由于![]() ,
,![]() ,
,![]() ,
,
所以,存在![]() ,使得
,使得![]() .
.
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增.
單調遞增.
故![]() ,不符合題意,
,不符合題意,
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)當a=-2時,求函數f(x)的極值;
(2)若ln[e(x+1)]≥2- f(-x)對任意的x∈[0,+∞)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學對函數![]() 進行研究后,得出以下結論,其中正確的有( )
進行研究后,得出以下結論,其中正確的有( )
A.函數![]() 的圖象關于原點對稱
的圖象關于原點對稱
B.對定義域中的任意實數![]() 的值,恒有
的值,恒有![]() 成立
成立
C.函數![]() 的圖象與
的圖象與![]() 軸有無窮多個交點,且每相鄰兩交點間距離相等
軸有無窮多個交點,且每相鄰兩交點間距離相等
D.對任意常數![]() ,存在常數
,存在常數![]() ,使函數
,使函數![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 和圓
和圓![]() ,傾斜角為45°的直線
,傾斜角為45°的直線![]() 過拋物線
過拋物線![]() 的焦點,且
的焦點,且![]() 與圓
與圓![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)動點![]() 在拋物線
在拋物線![]() 的準線上,動點
的準線上,動點![]() 在
在![]() 上,若
上,若![]() 在
在![]() 點處的切線
點處的切線![]() 交
交![]() 軸于點
軸于點![]() ,設
,設![]() .求證點
.求證點![]() 在定直線上,并求該定直線的方程.
在定直線上,并求該定直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年1月1日,我國開始施行《個人所得稅專項附加扣除操作辦法》,附加扣除的專項包括子女教育、繼續教育、大病醫療、住房貨款利息、住房租金、贍養老人.某單位有老年員工140人,中年員工180人,青年員工80人,現采用分層抽樣的方法,從該單位員工中抽取20人,調查享受個人所得稅專項附加扣除的情況,并按照員工類別進行各專項人數匯總,數據統計如下:
員工\人數\專項 | 子女教育 | 繼續教育 | 大病醫療 | 住房貸款利息 | 住房租金 | 贍養老人 |
老員工 | 4 | 0 | 2 | 2 | 0 | 3 |
中年員工 | 8 | 2 | 1 | 5 | 1 | 8 |
青年員工 | 1 | 2 | 0 | 1 | 2 | 1 |
(Ⅰ)在抽取的20人中,老年員工、中年員工、青年員工各有多少人;
(Ⅱ)從上表享受住房貨款利息專項扣除的員工中隨機選取2人,求選取2人都是中年員工的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦點在
的焦點在![]() 軸上,中心在坐標原點,拋物線
軸上,中心在坐標原點,拋物線![]() 的焦點在
的焦點在![]() 軸上,頂點在坐標原點,在
軸上,頂點在坐標原點,在![]() 、
、![]() 上各取兩個點,將其坐標記錄于表格中:
上各取兩個點,將其坐標記錄于表格中:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 、
、![]() 的標準方程;
的標準方程;
(2)已知定點![]() ,
,![]() 為拋物線
為拋物線![]() 上的一動點,過點
上的一動點,過點![]() 作拋物線
作拋物線![]() 的切線交橢圓
的切線交橢圓![]() 于
于![]() 、
、![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體![]() 棱長為
棱長為![]() ,如圖,
,如圖,![]() 為
為![]() 上的動點,
上的動點,![]() 平面
平面![]() .下面說法正確的是( )
.下面說法正確的是( )
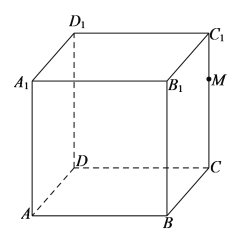
A.直線![]() 與平面
與平面![]() 所成角的正弦值范圍為
所成角的正弦值范圍為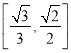
B.點![]() 與點
與點![]() 重合時,平面
重合時,平面![]() 截正方體所得的截面,其面積越大,周長就越大
截正方體所得的截面,其面積越大,周長就越大
C.點![]() 為
為![]() 的中點時,若平面
的中點時,若平面![]() 經過點
經過點![]() ,則平面
,則平面![]() 截正方體所得截面圖形是等腰梯形
截正方體所得截面圖形是等腰梯形
D.己知![]() 為
為![]() 中點,當
中點,當![]() 的和最小時,
的和最小時,![]() 為
為![]() 的中點
的中點
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面![]() ,B,
,B,![]() ,
,![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,則下列敘述錯誤的是( )
,則下列敘述錯誤的是( )
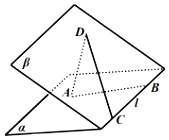
A.直線![]() 與
與![]() 是異面直線
是異面直線
B.直線![]() 在
在![]() 上的射影可能與
上的射影可能與![]() 平行
平行
C.過![]() 有且只有一個平面與
有且只有一個平面與![]() 平行
平行
D.過![]() 有且只有一個平面與
有且只有一個平面與![]() 垂直
垂直
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com