
給出定義在(0,+∞)上的三個函數:![]() ,
,![]() ,
,![]() ,已知
,已知![]() 在x=1處取極值.
在x=1處取極值.
(Ⅰ)確定函數h(x)的單調性;
(Ⅱ)求證:當![]() 時,恒有
時,恒有![]() 成立;
成立;
(Ⅲ)把函數h(x)的圖象向上平移6個單位得到函數h1(x)的圖象,試確定函數y=g(x)-h1(x)的零點個數,并說明理由.
(1)h(x)在(1,+∞)上是增函數,在(0,1)上是減函數.(2)見解析 (3)2
(Ⅰ)由題設,![]() ,則
,則![]() .
.
由已知,![]() ,即
,即![]() .
.
于是![]() ,則
,則![]() .
.
由![]() ,所以h(x)在(1,+∞)上是增函數,在(0,1)上是減函數.
,所以h(x)在(1,+∞)上是增函數,在(0,1)上是減函數.
(Ⅱ)當![]() 時,
時,![]() ,即
,即![]() .
.
欲證![]() ,只需證
,只需證![]() ,即證
,即證![]() .
.
設![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,所以
,所以![]() 在區間(1,e2)上為增函數.
在區間(1,e2)上為增函數.
從而當![]() 時,
時,![]() ,即
,即![]() ,故
,故![]() .
.
(Ⅲ)由題設,![]() .令
.令![]() ,則
,則
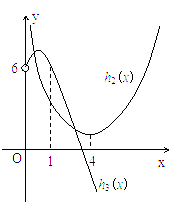
![]() ,即
,即![]() .
.
設![]() ,
,![]() ,則
,則
![]() ,由
,由![]() ,得x>4.
,得x>4.
所以![]() 在(4,+∞)上是增函數,在(0,4)上是減函數.
在(4,+∞)上是增函數,在(0,4)上是減函數.
又![]() 在(0,
在(0,![]() )上是增函數,在(
)上是增函數,在(![]() ,+∞)上是減函數.
,+∞)上是減函數.
因為當x→0時,![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() ,
,
![]() ,則函數
,則函數![]() 與
與![]() 的大致圖象如下:
的大致圖象如下:
由圖可知,當x>0時,兩個函數圖象有2個交點,故函數y=g(x)-h1(x)有2個零點.


科目:高中數學 來源: 題型:
| x |
| 2+f(x) |
| 2-f(x) |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分13分)
給出定義在(0,+∞)上的三個函數:![]() ,
,![]() ,
,![]() ,已知
,已知![]() 在x=1處取極值.
在x=1處取極值.
(Ⅰ)確定函數h(x)的單調性;
(Ⅱ)求證:當![]() 時,恒有
時,恒有![]() 成立;
成立;
(Ⅲ)把函數h(x)的圖象向上平移6個單位得到函數h1(x)的圖象,試確定函數y=g(x)-h1(x)的零點個數,并說明理由.
查看答案和解析>>
科目:高中數學 來源:湖南師大附中2010屆高三第一次模擬試卷數學(理) 題型:解答題
(本小題滿分13分)
給出定義在(0,+∞)上的三個函數: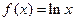 ,
,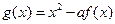 ,
,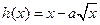 ,已知
,已知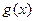 在x=1處取極值.
在x=1處取極值.
(Ⅰ)確定函數h(x)的單調性;
(Ⅱ)求證:當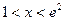 時,恒有
時,恒有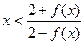 成立;
成立;
(Ⅲ)把函數h(x)的圖象向上平移6個單位得到函數h1(x)的圖象,試確定函數y=g(x)-h1(x)的零點個數,并說明理由.
查看答案和解析>>
科目:高中數學 來源:廣西省柳鐵一中2009-2010學年度高三年級5月份月考(理) 題型:解答題
(注意:在試題卷上作答無效)
給出定義在(0,+∞)上的三個函數: ,
,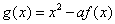 ,
, ,已知
,已知 在x=1處取極值.
在x=1處取極值.
(1)確定函數 的單調性;
的單調性;
(2)求證:當 時,恒有
時,恒有 成立;
成立;
(3)把函數 的圖象向上平移6個單位得到函數
的圖象向上平移6個單位得到函數 的圖象,試確定函數
的圖象,試確定函數 的零點個數,并說明理由.
的零點個數,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com