Question

兩封信隨機投入A、B、C三個空郵箱，則A郵箱的信件數ξ的數學期望E_ξ=    ；

Answer 1

【答案】分析：由題意知ξ的取值有0，1，2，當ξ=0時，表示的事件是A郵箱的信件數為0，由分步計數原理知兩封信隨機投入A、B、C三個空郵箱，共有3×3種結果，而滿足條件的A郵箱的信件數為0的結果數是2×2，由古典概型公式得到ξ=0時的概率，同理可得ξ=1時，ξ=2時，ξ=3時的概率，用期望公式得到結果．
解答：解：由題意知ξ的取值有0，1，2，
當ξ=0時，即A郵箱的信件數為0，
由分步計數原理知兩封信隨機投入A、B、C三個空郵箱，共有3×3種結果，
而滿足條件的A郵箱的信件數為0的結果數是2×2，
由古典概型公式得到ξ=0時的概率，同理可得ξ=1時，ξ=2時，ξ=3時的概率
，
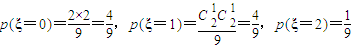
∴Eξ=
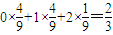
故答案為：．
點評：本題考查離散型隨機變量的期望，本題這種類型是近幾年高考題中經常出現的，考查離散型隨機變量的分布列和期望，大型考試中理科考試必出的一道問題．
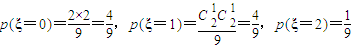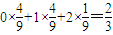