
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,曲線![]() 的參數方程為
的參數方程為![]() ,(
,( ![]() 為參數),以
為參數),以![]() 為極點,
為極點, ![]() 軸的正半軸建立極坐標系,曲線
軸的正半軸建立極坐標系,曲線![]() 是圓心在極軸上且經過極點的圓,射線
是圓心在極軸上且經過極點的圓,射線![]() 與曲線
與曲線![]() 交于點
交于點![]()
(Ⅰ)求曲線![]() 的普通方程及
的普通方程及![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在極坐標系中, ![]() 是曲線
是曲線![]() 的兩點,求
的兩點,求![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程選講
在直角坐標系![]() 中,曲線C1的參數方程為
中,曲線C1的參數方程為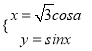 (a為參數),以原點O為極點,
(a為參數),以原點O為極點,
以x軸正半軸為極軸,建立極坐標系,曲 線C2的極坐標方程為![]()
(1)求曲線C1的普通方程與曲線C2的直角坐標方程.
(2)設P為曲線C1上的動點,求點P到C2上點的距離的最小值,并求此時點P坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年全國數學奧賽試行改革:在高二一年中舉行5次全區競賽,學生如果其中2次成績達全區前20名即可進入省隊培訓,不用參加其余的競賽,而每個學生最多也只能參加5次競賽.規定:若前4次競賽成績都沒有達全區前20名,則第5次不能參加競賽.假設某學生每次成績達全區前20名的概率都是![]() ,每次競賽成績達全區前20名與否互相獨立.
,每次競賽成績達全區前20名與否互相獨立.
(1)求該學生進入省隊的概率.
(2)如果該學生進入省隊或參加完5次競賽就結束,記該學生參加競賽的次數為![]() ,求
,求![]() 的分布列及
的分布列及![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著我國經濟的快速發展,民用汽車的保有量也迅速增長.機動車保有量的發展影響到環境質量、交通安全、道路建設等諸多方面.在我國,尤其是大中型城市,機動車已成為城市空氣污染的重要來源.因此,合理預測機動車保有量是未來進行機動車污染防治規劃、道路發展規劃等的重要前提.從2012年到2016年,根據“云南省某市國民經濟和社會發展統計公報”中公布的數據,該市機動車保有量數據如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代碼 | 1 | 2 | 3 | 4 | 5 |
機動車保有量 | 169 | 181 | 196 | 215 | 230 |
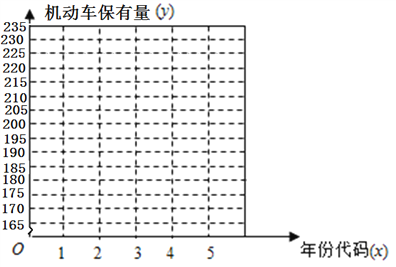
(1)在圖所給的坐標系中作出數據對應的散點圖;
(2)建立機動車保有量![]() 關于年份代碼
關于年份代碼![]() 的回歸方程;
的回歸方程;
(3)按照當前的變化趨勢,預測2017年該市機動車保有量.
附注:回歸直線方程![]() 中的斜率和截距的最小二乘估計公式分別為:
中的斜率和截距的最小二乘估計公式分別為:
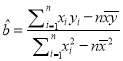 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定一個數列{an},在這個數列里,任取m(m≥3,m∈N*)項,并且不改變它們在數列{an}中的先后次序,得到的數列稱為數列{an}的一個m階子數列.已知數列{an}的通項公式為an=![]() (n∈N*,a為常數),等差數列a2,a3,a6是數列{an}的一個3階子數列.
(n∈N*,a為常數),等差數列a2,a3,a6是數列{an}的一個3階子數列.
(1)求a的值;
(2)等差數列b1,b2,…,bm是{an}的一個m (m≥3,m∈N*) 階子數列,且b1=![]() (k為常數,k∈N*,k≥2),求證:m≤k+1;
(k為常數,k∈N*,k≥2),求證:m≤k+1;
(3)等比數列c1,c2,…,cm是{an}的一個m (m≥3,m∈N*) 階子數列,
求證:c1+c2+…+cm≤2-![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的內角A,B,C所對的邊分別為a,b,c,滿足![]() .
.
(1)求角C的大小;
(2)設函數f(x)=cos(2x+C),將f(x)的圖象向右平移![]() 個單位長度后得到函數g(x)的圖象,求函數g(x)在區間
個單位長度后得到函數g(x)的圖象,求函數g(x)在區間![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分13分)已知動圓![]() 過定點
過定點![]() 且與
且與![]() 軸截得的弦
軸截得的弦![]() 的長為
的長為![]() .
.
(Ⅰ)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)已知點![]() ,動直線
,動直線![]() 和坐標軸不垂直,且與軌跡
和坐標軸不垂直,且與軌跡![]() 相交于
相交于![]() 兩點,試問:在
兩點,試問:在![]() 軸上是否存在一定點
軸上是否存在一定點![]() ,使直線
,使直線![]() 過點
過點![]() ,且使得直線
,且使得直線![]() ,
,![]() ,
,![]() 的斜率依次成等差數列?若存在,請求出定點
的斜率依次成等差數列?若存在,請求出定點![]() 的坐標;否則,請說明理由.
的坐標;否則,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 為遞增的等比數列,
為遞增的等比數列, ![]()
![]() ,
,
數列![]() 滿足
滿足![]() .
.
(Ⅰ)求數列![]() 的通項公式;(Ⅱ)求證:
的通項公式;(Ⅱ)求證: ![]() 是等差數列;
是等差數列;
(Ⅲ)設數列![]() 滿足
滿足![]() ,且數列
,且數列![]() 的前
的前![]() 項和
項和![]() ,并求使得
,并求使得![]() 對任意
對任意![]() 都成立的正整數
都成立的正整數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
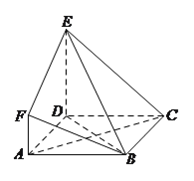
【題目】如圖,![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.
(Ⅰ)求證:![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)設點![]() 是線段
是線段![]() 上一個動點,試確定點
上一個動點,試確定點![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并證明你的結論.
,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com