Question

【題目】已知直線l：y=3x+3．
（1）求點P（5，3）關于直線l的對稱點P′的坐標；
（2）求直線l1：x﹣y﹣2=0關于直線l的對稱直線l2的方程；
（3）已知點M（2，6），試在直線l上求一點N使得|NP|+|NM|的值最小．

Answer 1

【答案】
（1）解：設點P的對稱點為P'（a，b），

則 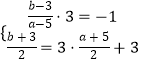，解得： ，

即點P'的坐標為（﹣4，6）；

（2）解：解方程組 得 ，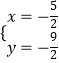

即兩直線l與l的交點坐標為

因為直線l與l2關于直線l對稱，所以直線l2必過點 ，

又由（1）可知，點P（5，3）恰好在直線l上，且其關于直線l的對稱點為P'（﹣4，6），

所以直線l2必過點P'（﹣4，6），這樣由兩點式可得： ，

即7x+y+22=0；

（3）解：由（1）得P'（﹣4，6），連接P'M，交直線l于N，連接NP，

則|NP|+|NM|=|NP'|+|NM|=|P'M|最小，

設出N（x，3x+3），則由P'，M，N共線，可得，

，解得，x=1，

則可得N（1，6）．

【解析】（1）設點P的對稱點為P'（a，b），由中點坐標公式和兩直線垂直的條件列方程，解出即可；（2）首先求出兩直線的交點，再由點關于直線對稱的求法求出對稱點，再由直線方程的形式，即可得到；（3）可由（1）的結論，連接P'M，交直線l于N，連接NP，再由三點共線的知識，即可求出N．