Question

已知二次函數y=f(x)在x=處取得最小值－ (t＞0),f(1)=0.

(1)求y=f(x)的表達式；

(2)若任意實數x都滿足等式f(x)·g(x)+a_nx+b_n=xⁿ⁺¹［g(x)］為多項式，n∈N^*),試用t表示a_n和b_n；

(3)設圓C_n的方程為(x－a_n)²+(y－b_n)²=r_n²，圓C_n與C_n+1外切(n=1,2,3,…);{r_n}是各項都是正數的等比數列，記S_n為前n個圓的面積之和，求r_n、S_n.

Answer 1

(1) f(x)=x²－(t+2)x+t+1, (2) a_n=［(t+1)ⁿ⁺¹－1］，b_n=［1－(t+1ⁿ), (3) r_n=, S_n=π(r₁²+r₂²+…+r_n²)=［(t+1)²ⁿ－1］

解析:

(1)設f(x)=a(x－)²－，由f(1)=0得a=1.

∴f(x)=x²－(t+2)x+t+1.

(2)將f(x)=(x－1)［x－(t+1)］代入已知得:

(x－1)［x－(t+1)］g(x)+a_nx+b_n=xⁿ⁺¹，

上式對任意的x∈R都成立，

取x=1和x=t+1分別代入上式得 

且t≠0，

解得a_n=［(t+1)ⁿ⁺¹－1］，b_n=［1－(t+1ⁿ)

(3)由于圓的方程為(x－a_n)²+(y－b_n)²=r_n²，

又由(2)知a_n+b_n=1，故圓C_n的圓心O_n在直線x+y=1上，

又圓C_n與圓C_n+1相切，故有r_n+r_n+1=｜a_n+1－a_n｜=(t+1)ⁿ⁺¹

設{r_n}的公比為q，則

                                                   

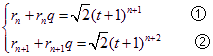
       ②÷①得q==t+1，代入①得r_n=

∴S_n=π(r₁²+r₂²+…+r_n²)=［(t+1)²ⁿ－1］.