Question

EC垂直Rt△ABC的兩條直角邊，D是斜邊AB的中點，AC=6，BC=8，EC=12，則DE的長為     ．

Answer 1

【答案】分析：由EC垂直Rt△ABC的兩條直角邊，可知EC⊥面ABC，再根據D是斜邊AB的中點，AC=6，BC=8，可求得CD的長，根據勾股定理可求得DE的長．
解答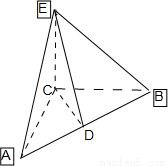：解：如圖，EC⊥AC，EC⊥CB，CB∩CA=C
∴EC⊥面ABC
而CD?面ABC
∴EC⊥CD
∵AC=6，BC=8，EC=12，△ABC是直角三角形，D是斜邊AB的中點，
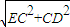
∴CD=5，ED==13
故答案為：13．
點評：考查線面垂直的判定和性質定理，利用勾股定理求線段的長度，屬基礎題．