Question

如圖，在直三棱柱ABC—A₁B₁C₁中，AB=BC，D、E分別為BB₁、AC₁的中點.

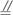
（1）證明：ED為異面直線BB₁與AC₁的公垂線；

（2）設AA₁=AC=AB，求二面角A₁—AD—C₁的大小.

Answer 1

（1）證明:如圖,設O為AC中點,連結EO、BO，則EOC₁C.又C₁CB₁B，∴EODB，EOBD為平行四邊形，ED∥OB.

∵AB=BC，∴BO⊥AC.

    又平面ABC⊥平面ACC₁A₁，BO面ABC，

    故BO⊥平面ACC₁A₁，

∴ED⊥平面ACC₁A₁，ED⊥AC₁，ED⊥CC₁.

∴ED⊥BB₁，ED為異面直線AC₁與BB₁的公垂線.

（2）解：連結A₁E.由AA₁=AC=AB可知，A₁ACC₁為正方形，∴A₁E⊥AC₁.

    又由ED⊥平面A₁ACC₁和ED平面ADC₁知平面ADC₁⊥平面A₁ACC₁，

∴A₁E⊥平面ADC₁.作EF⊥AD，垂足為F，連結A₁F，

    則A₁F⊥AD，∠A₁FE為二面角A₁—AD—C₁的平面角.

    不妨設AA₁=2,

    則AC=2，AB=，ED=OB=1，EF=，tanA₁FE=，

∴∠A₁FE=60°.

∴二面角A₁—AD—C₁為60°.