
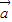 =(a1,a2),
=(a1,a2),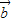 =(b1,b2),且
=(b1,b2),且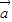 與
與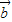 的夾角為θ,
的夾角為θ,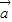 •
•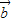 =|
=|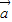 ||
||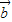 |cosθ,
|cosθ,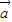 •
•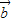 ≤|
≤|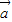 ||
||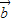 |.
|.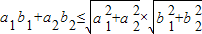 ,
,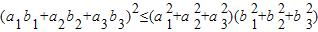 成立;
成立;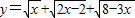 的最大值.
的最大值. •
•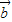 ≤|
≤|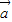 |•|
|•|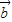 |,即可證明結論;
|,即可證明結論; =(1,1,1),
=(1,1,1),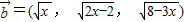 ,且
,且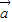 與
與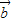 的夾角為θ,利用(I)的結論,即可得到結論.
的夾角為θ,利用(I)的結論,即可得到結論. =(a1,a2,a3),
=(a1,a2,a3),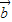 =(b1,b2,b3),且
=(b1,b2,b3),且 與
與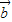 的夾角為θ,
的夾角為θ,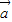 •
•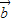 =|
=|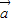 |•|
|•|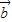 |cosθ,
|cosθ, •
•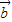 ≤|
≤| |•|
|•|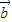 |,(3分)
|,(3分)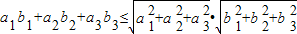 (6分)
(6分)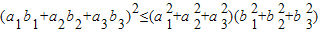 ,
,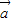 =(1,1,1),
=(1,1,1),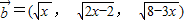 ,且
,且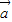 與
與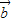 的夾角為θ,(9分)
的夾角為θ,(9分)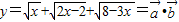 ,
,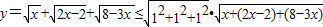 ,
, ,(12分)
,(12分) 與
與 共線,且方向相同)時,等號成立.
共線,且方向相同)時,等號成立.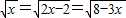 時,
時,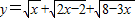 有最大值
有最大值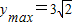 .(14分)
.(14分)

科目:高中數學 來源: 題型:閱讀理解
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
|
|
| a | 2 1 |
| a | 2 2 |
| a | 2 3 |
| b | 2 1 |
| b | 2 2 |
| b | 2 3 |
| x |
| 2x-2 |
| 8-3x |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
|
|
| a | 21 |
| a | 22 |
| a | 23 |
| b | 21 |
| b | 22 |
| b | 23 |
| x |
| 2x-2 |
| 8-3x |
查看答案和解析>>
科目:高中數學 來源: 題型:
請先閱讀:
設平面向量![]() =(a1,a2),
=(a1,a2),![]() =(b1,b2),且
=(b1,b2),且![]() 與
與![]() 的夾角為è,
的夾角為è,
因為![]() •
•![]() =|
=|![]() ||
||![]() |cosè,
|cosè,
所以![]() •
•![]() ≤|
≤|![]() ||
||![]() |.
|.
即![]() ,
,
當且僅當è=0時,等號成立.
(I)利用上述想法(或其他方法),結合空間向量,證明:對于任意a1,a2,a3,b1,b2,b3∈R,都有![]() 成立;
成立;
(II)試求函數![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com