
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
, ![]() ,離心率為
,離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,
上, ![]() ,
, ![]() ,過
,過![]() 與坐標軸不垂直的直線
與坐標軸不垂直的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() ,
, ![]() 的中點為
的中點為![]() ,在線段
,在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,求實數
?若存在,求實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】甲,乙兩臺機床同時生產一種零件,其質量按測試指標劃分:指標大于或等于95為正品,小于95為次品,現隨機抽取這兩臺車床生產的零件各100件進行檢測,檢測結果統計如下:
測試指標 |
|
|
|
|
|
機床甲 | 8 | 12 | 40 | 32 | 8 |
機床乙 | 7 | 18 | 40 | 29 | 6 |
(1)試分別估計甲機床、乙機床生產的零件為正品的概率;
(2)甲機床生產一件零件,若是正品可盈利160元,次品則虧損20元;乙機床生產一件零件,若是正品可盈利200元,次品則虧損40元,在(1)的前提下,現需生產這種零件2件,以獲得利潤的期望值為決策依據,應該如何安排生產最佳?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的短軸長為2,且函數
的短軸長為2,且函數![]() 的圖象與橢圓
的圖象與橢圓![]() 僅有兩個公共點,過原點的直線
僅有兩個公共點,過原點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點.
兩點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)點![]() 為線段
為線段![]() 的中垂線與橢圓
的中垂線與橢圓![]() 的一個公共點,求
的一個公共點,求![]() 面積的最小值,并求此時直線
面積的最小值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中, ![]() ,
, ![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻轉成
翻轉成![]() .若
.若![]() 為線段
為線段![]() 的中點,則在
的中點,則在![]() 翻折過程中:
翻折過程中:

①![]() 是定值;②點
是定值;②點![]() 在某個球面上運動;
在某個球面上運動;
③存在某個位置,使![]() ;④存在某個位置,使
;④存在某個位置,使![]() 平面
平面![]() .
.
其中正確的命題是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017 年省內某事業單位面向社會公開招騁工作人員,為保證公平競爭,報名者需要參加筆試和面試兩部分,且要求筆試成績必須大于或等于![]() 分的才有資格參加面試,
分的才有資格參加面試, ![]() 分以下(不含
分以下(不含![]() 分)則被淘汰,現有
分)則被淘汰,現有![]() 名競騁者參加筆試,參加筆試的成績按區間
名競騁者參加筆試,參加筆試的成績按區間![]() 分段,其頻率分布直方圖如圖所示(頻率分布直方圖有污損),但是知道參加面試的人數為
分段,其頻率分布直方圖如圖所示(頻率分布直方圖有污損),但是知道參加面試的人數為![]() ,且筆試成績在
,且筆試成績在![]() 的人數為
的人數為![]() .
.

(1)根據頻率分布直方圖,估算競騁者參加筆試的平均成績;
(2)若在面試過程中每人最多有![]() 次選題答題的機會,累計答對
次選題答題的機會,累計答對![]() 題或答錯
題或答錯![]() 題, 答對
題, 答對![]() 題者方可參加復賽,已知面試者甲答對每一個問題的概率都相同,并且相互之間沒有影響,若他連續三次答題中答對一次的概率為
題者方可參加復賽,已知面試者甲答對每一個問題的概率都相同,并且相互之間沒有影響,若他連續三次答題中答對一次的概率為![]() ,求面試者甲答題個數
,求面試者甲答題個數![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電子原件生產廠生產的10件產品中,有8件一級品,2件二級品,一級品和二級品在外觀上沒有區別.從這10件產品中任意抽檢2件,計算:
(1)2件都是一級品的概率;
(2)至少有一件二級品的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
: ![]() ,定點
,定點![]() (常數
(常數![]() )的直線
)的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 、
、![]() 兩點.
兩點.
(1)若點![]() 的坐標為
的坐標為![]() ,求證:
,求證: ![]()
(2)若![]() ,以
,以![]() 為直徑的圓的位置是否恒過一定點?若存在,求出這個定點,若不存在,請說明理由.
為直徑的圓的位置是否恒過一定點?若存在,求出這個定點,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2016-2017學年遼寧省六校協作體高二下學期期初數學(理)】已知圓![]() 的圓心在坐標原點,且與直線
的圓心在坐標原點,且與直線![]() 相切.
相切.
(1)求直線![]() 被圓
被圓![]() 所截得的弦
所截得的弦![]() 的長;
的長;
(2)過點![]() 作兩條與圓
作兩條與圓![]() 相切的直線,切點分別為
相切的直線,切點分別為![]() 求直線
求直線![]() 的方程;
的方程;
(3)若與直線![]() 垂直的直線
垂直的直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,若
,若![]() 為鈍角,求直線
為鈍角,求直線![]() 在
在![]() 軸上的截距的取值范圍.
軸上的截距的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD,PD⊥底面ABCD,且底面ABCD是邊長為2的正方形,M、N分別為PB、PC的中點. 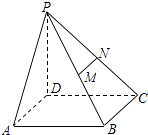
(1)證明:MN∥平面PAD;
(2)若PA與平面ABCD所成的角為45°,求四棱錐P﹣ABCD的體積V.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com