
已知數列{an}滿足條件:a1=1,a2=r(r>0)且{anan+1}是公比為q(q>0)的等比數列.設bn=a2n-1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2>an+2an+3(n∈N)成立的q的取值范圍;
(2)求![]()
![]() ,其中Sn=b1+b2+…+bn.
,其中Sn=b1+b2+…+bn.
解:(1)∵{anan+1}是公比為q的等比數列,且a1=1,a2=r,
∴anan+1=rqn-1.
∵anan+1+an+1an+2>an+2an+3,
∴rqn-1+rqn>rqn+1.
∵r>0,q>0,∴1+q>q2.
解得![]() <q<
<q<![]() .
.
∴0<q<![]() .
.
(2)∵a2n-1a2n=rq2n-2,∴a2n=![]() . ①
. ①
∵a2n-1a2n-2= rq2n-3,
∴a2n-1=![]() . ②
. ②
由①②可得a2n=qa2n-2. ③
同理a2n-1=qa2n-3. ④
∴bn=a2n-1+a2n
=qa2n-3+qa2n-2
=q(a2n-3+a2n-2)
=qbn-1.
∴{bn}是公比為q的等比數列.
∴bn=(a1+a2)qn-1= (1+r)qn-1.
∴Sn=b1+b2+…+bn
=(1+r)+(1+r) q+…+(1+r)qn-1
=(1+r) (1+q+…+qn-1).
當0<q<1時,![]()
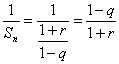 ;
;
當q=1時,![]()
![]() =
=![]()
![]() =0;
=0;
當q>1時,Sn=(1+r)(1+q+…+qn-1)=(1+r)![]() ,
,
![]()
![]() =
=![]()
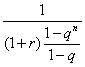 =
=![]()
![]() =0.
=0.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:
| 3+4an |
| 12-4an |
| 1 | ||
an-
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 5 | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com