
【題目】已知函數f(x)=x|x﹣2|.
(1)作出函數f(x)=x|x﹣2|的大致圖象;
(2)若方程f(x)﹣k=0有三個解,求實數k的取值范圍.
(3)若x∈(0,m](m>0),求函數y=f(x)的最大值.
【答案】
(1)解:函數f(x)=x|x﹣2|= 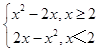 ,
,
由分段函數的畫法,可得如圖
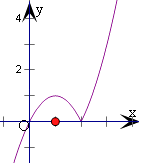
(2)解:若方程f(x)﹣k=0有三個解,即函數f(x)圖象與直線y=k有三個交點,
由圖可得,當0<k<1時,有三個交點,即方程f(x)﹣k=0有三個解
(3)解:當0<m≤1時,f(x)在(0,m]遞增,f(m)取得最大值,且為2m﹣m2;
由x2﹣2x=1,解得x=1+ ![]() (1﹣
(1﹣ ![]() 舍去),
舍去),
當1<m≤1+ ![]() 時,由f(x)的圖象可得f(1)取得最大值1;
時,由f(x)的圖象可得f(1)取得最大值1;
當m>1+ ![]() 時,由f(x)的圖象可得f(m)取得最大值m2﹣2m.
時,由f(x)的圖象可得f(m)取得最大值m2﹣2m.
綜上可得,當0<m≤1時,f(x)的最大值為2m﹣m2;
當1<m≤1+ ![]() 時,f(x)的最大值為1;
時,f(x)的最大值為1;
當m>1+ ![]() 時,f(x)的最大值為m2﹣2m.
時,f(x)的最大值為m2﹣2m.
【解析】(1)寫出f(x)的分段形式,畫出圖象;(2)由題意可得,函數f(x)圖象與直線y=k有三個交點,通過平移直線y=k,即可得到k 范圍;(3)對m討論,分當0<m≤1時,當1<m≤1+ ![]() 時,當m>1+
時,當m>1+ ![]() 時,三種情況,通過圖象和單調性,即可得到最大值.
時,三種情況,通過圖象和單調性,即可得到最大值.


科目:高中數學 來源: 題型:
【題目】若二次函數![]() 的圖象和直線
的圖象和直線![]() 無交點,現有下列結論:
無交點,現有下列結論:
①方程![]() 一定沒有實數根;②若
一定沒有實數根;②若![]() ,則不等式
,則不等式![]() 對一切實數
對一切實數![]() 都成立;
都成立;
③若![]() ,則必存在實數
,則必存在實數![]() ,使
,使![]() ;④若
;④若![]() ,則不等式
,則不等式![]() 對一切實數都成立;⑤函數
對一切實數都成立;⑤函數![]() 的圖象與直線
的圖象與直線![]() 也一定沒有交點,其中正確的結論是__________.(寫出所有正確結論的編號)
也一定沒有交點,其中正確的結論是__________.(寫出所有正確結論的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的偶函數
上的偶函數![]() ,其導函數為
,其導函數為![]() ,若對任意的實數
,若對任意的實數![]() ,都有
,都有![]() 恒成立,則使
恒成立,則使![]() 成立的實數
成立的實數![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B. (﹣∞,﹣1)∪(1,+∞)
B. (﹣∞,﹣1)∪(1,+∞)
C. (﹣1,1) D. (﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (b≠0且b是常數).
(b≠0且b是常數).
(1)如果方程f(x)=x有唯一解,求b值.
(2)在(1)的條件下,求證:f(x)在(﹣∞,﹣1)上是增函數;
(3)若函數f(x)在(1,+∞)上是減函數,求負數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列函數:①f(x)=3|x| , ②f(x)=x3 , ③f(x)=ln ![]() ,④f(x)=
,④f(x)= ![]() ,⑤f(x)=﹣x2+1中,既是偶函數,又是在區間(0,+∞)上單調遞減函數為 . (寫出符合要求的所有函數的序號).
,⑤f(x)=﹣x2+1中,既是偶函數,又是在區間(0,+∞)上單調遞減函數為 . (寫出符合要求的所有函數的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王于年初用50萬元購買一輛大貨車,第一年因繳納各種費用需支出6萬元,從第二年起,每年都比上一年增加支出2萬元,假定該車每年的運輸收入均為25萬元.小王在該車運輸累計收入超過總支出后,考慮將大貨車作為二手車出售,若該車在第x年年底出售,其銷售價格為(25-x)萬元(國家規定大貨車的報廢年限為10年).
(1)大貨車運輸到第幾年年底,該車運輸累計收入超過總支出?
(2)在第幾年年底將大貨車出售,能使小王獲得的年平均利潤最大?(利潤=累計收入+銷售收入-總支出)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() ﹣
﹣ ![]()
(1)證明函數f(x)是奇函數;
(2)證明函數f(x)在(﹣∞,+∞)內是增函數;
(3)求函數f(x)在[1,2]上的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com