
【題目】誠信是立身之本,道德之基,我校學生會創設了“誠信水站”,既便于學生用水,又推進誠信教育,并用“![]() ”表示每周“水站誠信度”,為了便于數據分析,以四周為一周期,如表為該水站連續十二周(共三個周期)的誠信數據統計:
”表示每周“水站誠信度”,為了便于數據分析,以四周為一周期,如表為該水站連續十二周(共三個周期)的誠信數據統計:
第一周 | 第二周 | 第三周 | 第四周 | |
第一周期 |
|
|
|
|
第二周期 |
|
|
|
|
第三周期 |
|
|
|
|
(Ⅰ)計算表中十二周“水站誠信度”的平均數![]() ;
;
(Ⅱ)若定義水站誠信度高于![]() 的為“高誠信度”,
的為“高誠信度”,![]() 以下為“一般信度”則從每個周期的前兩周中隨機抽取兩周進行調研,計算恰有兩周是“高誠信度”的概率;
以下為“一般信度”則從每個周期的前兩周中隨機抽取兩周進行調研,計算恰有兩周是“高誠信度”的概率;
(Ⅲ)已知學生會分別在第一個周期的第四周末和第二個周期的第四周末各舉行了一次“以誠信為本”的主題教育活動,根據已有數據,說明兩次主題教育活動的宣傳效果,并根據已有數據陳述理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)兩次活動效果均好,理由詳見解析.
;(Ⅲ)兩次活動效果均好,理由詳見解析.
【解析】
(Ⅰ)結合表中的數據,代入平均數公式求解即可;
(Ⅱ)設抽到“高誠信度”的事件為![]() ,則抽到“一般信度”的事件為
,則抽到“一般信度”的事件為![]() ,則隨機抽取兩周,則有兩周為“高誠信度”事件為
,則隨機抽取兩周,則有兩周為“高誠信度”事件為![]() ,利用列舉法列出所有的基本事件和事件
,利用列舉法列出所有的基本事件和事件![]() 所包含的基本事件,利用古典概型概率計算公式求解即可;
所包含的基本事件,利用古典概型概率計算公式求解即可;
(Ⅲ)結合表中的數據判斷即可.
(Ⅰ)表中十二周“水站誠信度”的平均數
![]() .
.
(Ⅱ)設抽到“高誠信度”的事件為![]() ,則抽到“一般信度”的事件為
,則抽到“一般信度”的事件為![]() ,則隨機抽取兩周均為“高誠信度”事件為
,則隨機抽取兩周均為“高誠信度”事件為![]() ,總的基本事件為
,總的基本事件為![]() 共15種,
共15種,
事件![]() 所包含的基本事件為
所包含的基本事件為![]() 共10種,
共10種,
由古典概型概率計算公式可得,![]() .
.
(Ⅲ)兩次活動效果均好.
理由:活動舉辦后,“水站誠信度'由![]() 和
和![]()
![]()
![]() 看出,后繼一周都有提升.
看出,后繼一周都有提升.


科目:高中數學 來源: 題型:
【題目】松、竹、梅經冬不衰,因此有“歲寒三友”之稱.在我國古代的詩詞和典籍中有很多與松和竹相關的描述和記載,宋代劉學箕的《念奴嬌·水軒沙岸》的“綴松黏竹,恍然如對三絕”描寫了大雪后松竹并生相依的美景;宋元時期數學名著《算學啟蒙》中亦有關于“松竹并生”的問題:松長五尺,竹長兩尺,松日自半,竹日自倍,松竹何日而長等.現欲知幾日后,竹長超過松長一倍.為了解決這個新問題,設計下面的程序框圖,若輸入的![]() ,
,![]() ,則輸出的
,則輸出的![]() 的值為( )
的值為( )
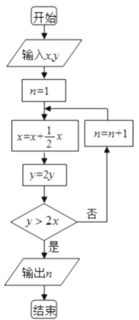
A.4B.5C.6D.7
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有4名同學去參加校學生會活動,共有甲、乙兩類活動可供參加者選擇,為增加趣味性,約定:每個人通過擲一枚質地均勻的骰子決定自己去參加哪類活動,擲出點數為1或2的人去參加甲類活動,擲出點數大于2的人去參加乙類活動.
(1)求這4個人中恰有2人去參加甲類活動的概率;
(2)用![]() ,
,![]() 分別表示這4個人中去參加甲、乙兩類活動的人數.記
分別表示這4個人中去參加甲、乙兩類活動的人數.記![]() ,求隨機變量
,求隨機變量![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比數列.
成等比數列.
(1)求數列![]() 的通項公式;
的通項公式;
(2)記![]() 為數列
為數列![]() 的前
的前![]() 項和,是否存在正整數
項和,是否存在正整數![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩個班級均為 40 人,進行一門考試后,按學生考試成績及格與不及格進行統計,甲班及格人數為 36 人,乙班及格人數為 24 人.
(1)根據以上數據建立一個2![]() 2的列聯表;
2的列聯表;
(2)試判斷是否成績與班級是否有關?
參考公式:![]() ;
;![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面有四個關于充要條件的命題:①“向量![]() 與非零向量
與非零向量![]() 共線”的充要條件是“有且只有一個實數
共線”的充要條件是“有且只有一個實數![]() 使得
使得![]() ;②“函數
;②“函數![]() 為偶函數”的充要條件是“
為偶函數”的充要條件是“![]() ”;③“兩個事件為互斥事件”是“這兩個事件為對立事件”的充要條件;④設
”;③“兩個事件為互斥事件”是“這兩個事件為對立事件”的充要條件;④設![]() ,則“
,則“![]() "是“
"是“![]() 為偶函數”的充分不必要條件.其中,真命題的序號是____.
為偶函數”的充分不必要條件.其中,真命題的序號是____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 過定點
過定點![]() 且與
且與![]() 軸相切,點
軸相切,點![]() 關于圓心
關于圓心![]() 的對稱點為
的對稱點為![]() ,點
,點![]() 的軌跡為
的軌跡為![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)一條直線經過點![]() ,且交曲線
,且交曲線![]() 于
于![]() 、
、![]() 兩點,點
兩點,點![]() 為直線
為直線![]() 上的動點.
上的動點.
①求證:![]() 不可能是鈍角;
不可能是鈍角;
②是否存在這樣的點![]() ,使得
,使得![]() 是正三角形?若存在,求點
是正三角形?若存在,求點![]() 的坐標:否則,說明理由.
的坐標:否則,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com