
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間和極值;
的單調區間和極值;
(2)若![]() 恒成立;求實數
恒成立;求實數![]() 的值.
的值.
【答案】(1)函數![]() 的減區間為
的減區間為![]() ,增區間為
,增區間為![]() ,極小值為
,極小值為![]() ,無極大值;(2)
,無極大值;(2)![]() .
.
【解析】
試題分析:(1)求出導數![]() 及定義域,在定義域內解不等式
及定義域,在定義域內解不等式![]() 得增區間,解不等式
得增區間,解不等式![]() 得減區間,同時可確定極值;(2)設
得減區間,同時可確定極值;(2)設![]() ,求出導數
,求出導數![]() ,研究
,研究![]() 的單調性,不等式
的單調性,不等式![]() 恒成立,即
恒成立,即![]() 的最小值非負,因此由導數求得
的最小值非負,因此由導數求得![]() 的最小值,由于
的最小值,由于![]() ,因此當
,因此當![]() 時,
時,![]() 單調遞增,不合題意(
單調遞增,不合題意(![]() ),
),![]() 時,
時,![]() ,再由函數
,再由函數![]() 的單調性可得只有
的單調性可得只有![]() 時,
時,![]()
![]() ,從而確定
,從而確定![]() .
.
試題解析:(1)注意到函數![]() 的定義域為
的定義域為![]() ,
,
當![]() 時,
時,![]() ,若
,若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() .
.
所以![]() 是
是![]() 上的減函數,是
上的減函數,是![]() 上的增函數,故
上的增函數,故![]() ,故函數
,故函數![]() 的減區間為
的減區間為![]() ,增區間為
,增區間為![]() ,極小值為
,極小值為![]() ,無極大值.
,無極大值.
(2)由(1)知![]() ,當
,當![]() 時,
時,![]() 時,
時,![]() 是
是![]() 上的增函數,注意到
上的增函數,注意到![]() 時,
時,![]() ,不合題意.當
,不合題意.當![]() 時,若
時,若![]() ;若
;若![]() .所以
.所以![]() 是
是![]() 上的減函數,是
上的減函數,是![]() 上的增函數,故只需
上的增函數,故只需![]() .令
.令![]() ,當
,當![]() 時,
時,
![]() ;當
;當![]() 時,
時,![]() .所以
.所以![]() 是
是![]() 上的減函數,是
上的減函數,是![]() 上的增函數.
上的增函數.
故![]() 當且僅當
當且僅當![]() 時等號成立. 即
時等號成立. 即![]() 所求.
所求.


 快捷英語周周練系列答案
快捷英語周周練系列答案科目:高中數學 來源: 題型:
【題目】某單位員工![]() 人參加“學雷鋒”志愿活動,按年齡分組:第組
人參加“學雷鋒”志愿活動,按年齡分組:第組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.

(1)下表是年齡的頻率分布表,求正整數![]() 的值;
的值;
區間 |
|
|
|
|
|
人數 |
|
|
|
|
|
(2)現在要從年齡較小的第![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 人,年齡在第
人,年齡在第![]() 組抽取的員工的人數分別是多少?
組抽取的員工的人數分別是多少?
(3)在(2)的前提下,從這![]() 人中隨機抽取
人中隨機抽取![]() 人參加社區宣傳交流活動,求至少有人年齡在第
人參加社區宣傳交流活動,求至少有人年齡在第![]() 組的概率.
組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線C的極坐標方程是ρ=2cosθ,以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線L的參數方程是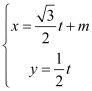 (t為參數).
(t為參數).
(1)求曲線C的直角坐標方程和直線L的普通方程;
(2)設點P(m,0),若直線L與曲線C交于A,B兩點,且|PA||PB|=1,求實數m的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中是公理的是
A. 在空間中,如果兩個角的兩條邊對應平行,那么這兩個角相等或互補
B. 如果一個平面經過另一個平面的一條垂線,那么這兩個平面互相垂直
C. 平行于同一條直線的兩條直線平行
D. 如果兩個平行平面同時與第三個平面相交,那么它們的交線平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個年級有12個班,每個班有50名學生,按1到50排學號,為了交流學習經驗,要求每班學號為14的學生留下進行交流,這里運用的是( )
A. 分層抽樣 B. 抽簽法
C. 隨機數表法 D. 系統抽樣
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com