
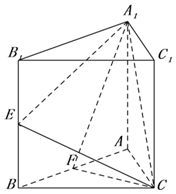
 正三棱柱ABC-A1B1C1底邊長為2,E,F分別為BB1,AB的中點.
正三棱柱ABC-A1B1C1底邊長為2,E,F分別為BB1,AB的中點.分析 (I)取B1A1中點為N,連結BN,推導出BN∥A1F,從而EM∥BN,進而EM∥A1F,由此能證明EM∥面A1FC.
(II)以F為坐標原點建立空間直角坐標系,設AA1=a,利用向量法能求出結果.
解答 證明:(I)取B1A1中點為N,連結BN,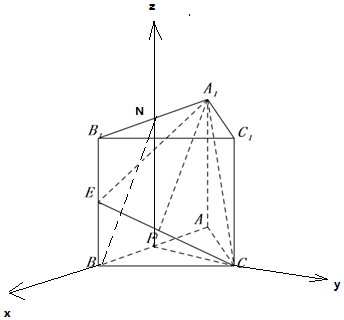
則BN∥A1F,又B1A1=4B1M,
則EM∥BN,所以EM∥A1F,
因為EM?面A1FC,A1F?面A1FC,
故EM∥面A1FC.
解:(II)如圖,以F為坐標原點建立空間直角坐標系,設AA1=a.
則$F(0,0,0),{A_1}(-1,0,a),E(1,0,\frac{a}{2}),C(0,\sqrt{3},0)$,
$\overrightarrow{EC}=(-1,\sqrt{3},-\frac{a}{2}),\overrightarrow{FC}=(0,\sqrt{3},0),\overrightarrow{{A_1}E}=(2,0,-\frac{a}{2}),\overrightarrow{{A_1}C}=(1,\sqrt{3},-a)$,
設平面A1CF法向量為$\overrightarrow m=(x,y,z)$,
設平面A1CE法向量為$\overrightarrow n=(x,y,z)$.
則$\left\{\begin{array}{l}\overrightarrow{{A_1}C}•\overrightarrow m=x+\sqrt{3}y-az=0\\ \overrightarrow{FC}•\overrightarrow m=\sqrt{3}y=0\end{array}\right.$,取z=1,得$\overrightarrow m=(a,0,1)$,
$\left\{\begin{array}{l}\overrightarrow{{A_1}C}•\overrightarrow n=x+\sqrt{3}y-az=0\\ \overrightarrow{{A_1}E}•\overrightarrow n=2x-\frac{a}{2}z=0\end{array}\right.$,取x=a,得$\overrightarrow n=(a,\sqrt{3}a,4)$;
設二面角E-A1C-F的平面角為θ,
∵二面角E-A1C-F所成角的余弦值為$\frac{{2\sqrt{7}}}{7}$,
∴$cosθ=cos<\overrightarrow m,\overrightarrow n>=\frac{{{a^2}+4}}{{\sqrt{{a^2}+1}•\sqrt{4{a^2}+16}}}=\frac{{2\sqrt{7}}}{7}$,
整理,得a2=$\frac{4}{3}$,∴a=$\frac{2\sqrt{3}}{3}$,
故當二面角E-A1C-F所成角的余弦值為$\frac{{2\sqrt{7}}}{7}$時,AA1的值為$\frac{2\sqrt{3}}{3}$.
點評 本題考查線面平行的證明,考查滿足條件的線段長的求法,是中檔題,解題時要認真審題,注意向量法的合理運用.


 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1)(2) | B. | (2)(3) | C. | (1)(3) | D. | (2)(4) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 綜合法 | B. | 分析法 | ||
| C. | 綜合法,分析法結合使用 | D. | 其他證法 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 23 | B. | 20 | C. | 21 | D. | 19 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com