已知命題p:點A(x,y)在圓(x-1)2+(y-1)2=1外,若命題p是假命題,則z=x+y的最小值為________.
2
分析:由命題p:點A(x,y)在圓(x-1)
2+(y-1)
2=1外,且命題p是假命題,知點A(x,y)在圓(x-1)
2+(y-1)
2=1內或點A(x,y)在圓(x-1)
2+(y-1)
2=1上,由此利用線性規劃能求出z=x+y的最小值.
解答:∵命題p:點A(x,y)在圓(x-1)
2+(y-1)
2=1外,
且命題p是假命題,
∴點A(x,y)在圓(x-1)
2+(y-1)
2=1內或點A(x,y)在圓(x-1)
2+(y-1)
2=1上,
如圖,
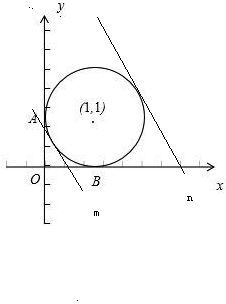
斜率為-1的切線m,n與圓有兩個切點,其中m與圓的切點使得z取最小值,
n與圓的切點使得z取最大值,
∵O(0,0)與圓心(1,1)的斜率為k=1,
∴m,n與圓的切點分別是O(0,0)與圓心(1,1)的連線y=x與圓(x-1)
2+(y-1)
2=1的兩個交點,
解方程組
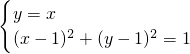
,得(1-

,1-

),(1+

,1+

)
∴在點(1-

,1-

)處,z=x+y取最小值2.
故答案為:2.
點評:本題考查命題的真假判斷與應用,是基礎題.解題時要認真審題,仔細解答,注意線性規劃的合理運用.


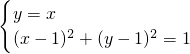 ,得(1-
,得(1- ,1-
,1- ),(1+
),(1+ ,1+
,1+ )
) ,1-
,1- )處,z=x+y取最小值2.
)處,z=x+y取最小值2.

 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案