【題目】設函數
（Ⅰ）當
（
為自然對數的底數）時，求
的極小值；
（Ⅱ）若函數
存在唯一零點，求
的取值范圍．
【答案】（Ⅰ）
的極小值為2；（Ⅱ）當
或
時，函數
有且只有一個零點.
【解析】試題分析：（1）先求導數，再求導函數零點，列表分析導函數符號變化規律，進而確定極值（2）先化簡
，再利用參變分離法得
，利用導數研究函數
，由圖像可得存在唯一零點時
的取值范圍
試題解析：（1）由題設，當
時， 
，
則
，由
，得
．
∴當
， 
， 
在
上單調遞減，
當
， 
， 
在
上單調遞增，
∴當
時， 
取得極小值
，
∴
的極小值為2.
（2）由題設
，
令
，得
．
設
，則
，
當
時， 
， 
在
上單調遞增；
當
時， 
， 
在
上單調遞減．
∴
是
的唯一極值點，且是極大值點，因此
也是
的最大值點．
∴
的最大值為
．
又
，結合
的圖象（如圖），可知
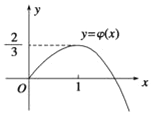
當
時，函數
有且只有一個零點；
當
時，函數
有且只有一個零點．
所以，當
或
時，函數
有且只有一個零點.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】假定下述數據是甲、乙兩個供貨商的交貨天數：
甲：10 9 10 10 11 11 9 11 10 10
乙：8 10 14 7 10 11 10 8 15 12
估計兩個供貨商的交貨情況，并問哪個供貨商交貨時間短一些，哪個供貨商交貨時間較具一致性與可靠性．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于定義域為
的函數
，若滿足①
；②當
，且
時，都有
；③當
，且
時， 
，則稱
為“偏對稱函數”．現給出四個函數：
①
； ② 
；
③
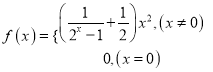； ④
．
則其中是“偏對稱函數”的函數為__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，AB為圓O的直徑，點E、F在圓O上，AB ∥EF，矩形ABCD所在平面與圓O所在的平面互相垂直．已知AB＝2，EF＝1.
(1)求證：平面DAF⊥平面CBF；
(2)求直線AB與平面CBF所成角的大小；
(3)求AD的長為何值時，平面DFC與平面FCB所成的銳二面角的大小為60°？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的左，右焦點分別為
，且
與短軸的一個端點Q構成一個等腰直角三角形，點P（
）在橢圓
上，過點
作互相垂直且與x軸不重合的兩直線AB，CD分別交橢圓
于A，B，C，D且M，N分別是弦AB，CD的中點
(1)求橢圓的方程
(2)求證：直線MN過定點R（
）
(3)求
面積的最大值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
