
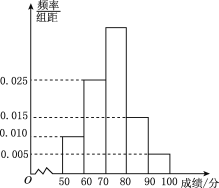
【題目】從2013年開始,國家教育部要求高中階段每學年都要組織學生進行學生體質健康測試,方案要求以學校為單位組織實施,某校對高一(1)班學生根據《國家學生體質健康標準》的測試項目按百分制進行了預備測試,并對50分以上的成績進行統計,其頻率分布直方圖如圖.所示,已知[90,100]分數段的人數為2.
(1)求[70,80)分數段的人數;
(2)現根據預備測試成績從成績在80分以上(含80分)的學生中任意選出2人代表班級參加學校舉行的一項體育比賽,求這2人的成績一個在[80,90)分數段、一個在[90,100]分數段的概率.
【答案】(1)18;(2)![]()
【解析】
⑴由頻率分布直方圖可知,各個分數段的頻率,求出![]() 分以上的總人數,
分以上的總人數,![]() 分數段的頻率,即可求出人數
分數段的頻率,即可求出人數
⑵求得![]() 分數段的人數,列舉出所有可能性情況,然后計算結果
分數段的人數,列舉出所有可能性情況,然后計算結果
(1)由頻率分布直方圖可知,[90,100]分數段的頻率為0.005×10=0.05,
[70,80)分數段的頻率為1-(0.010+0.025+0.015+0.005)×10=0.45,
因為[90,100]分數段的人數為2,所以50分以上的總人數為![]() =40,
=40,
所以[70,80)分數段的人數為40×0.45=18.
(2)由(1)可求得[80,90)分數段的人數為40×0.15=6,
設[80,90)分數段的6名學生分別為A1,A2,A3,A4,A5,A6,[90,100]分數段的2名學生分別為B1,B2,
則從中選出2人的選法有(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,A6),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,A5),(A2,A6),(A2,B1),(A2,B2),(A3,A4),(A3,A5),(A3,A6),(A3,B1),(A3,B2),(A4,A5),(A4,A6),(A4,B1),(A4,B2),(A5,A6),(A5,B1),(A5,B2),(A6,B1),(A6,B2),(B1,B2),共28種.
其中這2人的成績一個在[80,90)分數段、一個在[90,100]分數段的情況有(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(A5,B1),(A5,B2),(A6,B1),(A6,B2),共12種,
則所求概率P=![]() =
=![]() .
.


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目:高中數學 來源: 題型:
【題目】受電視機在保修期內維修費等因素的影響,企業生產每臺電視機的利潤與該電視機首次出現故障的時間有關.某電視機制造廠生產甲、乙兩種型號電視機,保修期均為2年,現從該廠已售出的兩種型號電視機中各隨機抽取50臺,統計數據如下:
品牌 | 甲 | 乙 | |||
首次出現故障時間x(年) |
|
|
|
|
|
電視機數量(臺) | 3 | 5 | 42 | 8 | 42 |
每臺利潤(千元) | 1 | 2 | 3 | 1.8 | 2.8 |
將頻率視為概率,解答下列問題:
(1)從該廠生產的甲種型號電視機中隨機抽取一臺,求首次出現故障發生在保修期內的概率;
(2)該廠預計今后這兩種型號電視機銷量相當,由于資金限制,只能生產其中一種型號電視機,若從經濟效益的角度考慮,你認為應該產生哪種型號電視機?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
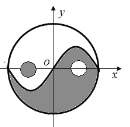
【題目】太極是中國古代的哲學術語,意為派生萬物的本源.太極圖是以黑白兩個魚形紋組成的圓形圖案,俗稱陰陽魚.太極圖形象化地表達了陰陽輪轉,相反相成是萬物生成變化根源的哲理.太極圖形展現了一種互相轉化,相對統一的形式美.按照太極圖的構圖方法,在平面直角坐標系中,圓![]() 被
被![]() 的圖象分割為兩個對稱的魚形圖案,圖中的兩個一黑一白的小圓通常稱為“魚眼”,已知小圓的半徑均為
的圖象分割為兩個對稱的魚形圖案,圖中的兩個一黑一白的小圓通常稱為“魚眼”,已知小圓的半徑均為![]() ,現在大圓內隨機投放一點,則此點投放到“魚眼”部分的概率為( )
,現在大圓內隨機投放一點,則此點投放到“魚眼”部分的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,從流水線上隨機抽取![]() 件產品,統計其質量指標值并繪制頻率分布直方圖(如圖1):規定產品的質量指標值在
件產品,統計其質量指標值并繪制頻率分布直方圖(如圖1):規定產品的質量指標值在![]() 的為劣質品,在
的為劣質品,在![]() 的為優等品,在
的為優等品,在![]() 的為特優品,銷售時劣質品每件虧損
的為特優品,銷售時劣質品每件虧損![]() 元,優等品每件盈利
元,優等品每件盈利![]() 元,特優品每件盈利
元,特優品每件盈利![]() 元,以這
元,以這![]() 件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
件產品的質量指標值位于各區間的頻率代替產品的質量指標值位于該區間的概率.
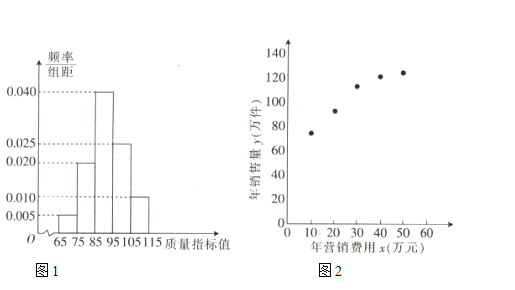
(1)求每件產品的平均銷售利潤;
(2)該企業主管部門為了解企業年營銷費用![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:萬件)的影響,對該企業近
(單位:萬件)的影響,對該企業近![]() 年的年營銷費用
年的年營銷費用![]() 和年銷售量
和年銷售量![]() ,
,![]() 數據做了初步處理,得到的散點圖(如圖2)及一些統計量的值.
數據做了初步處理,得到的散點圖(如圖2)及一些統計量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根據散點圖判斷,![]() 可以作為年銷售量
可以作為年銷售量![]() (萬件)關于年營銷費用
(萬件)關于年營銷費用![]() (萬元)的回歸方程.
(萬元)的回歸方程.
①求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
②用所求的回歸方程估計該企業每年應投入多少營銷費,才能使得該企業的年收益的預報值達到最大?(收益![]() 銷售利潤
銷售利潤![]() 營銷費用,取
營銷費用,取![]() )
)
附:對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為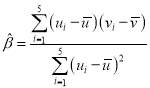 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一塊各面均涂有油漆的正方體被鋸成27個大小相同的小正方體,若將這些小正方體均勻地攪混在一起,從中任意取出一個,則取出的小正方體兩面涂有油漆的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科研課題組通過一款手機APP軟件,調查了某市1000名跑步愛好者平均每周的跑步量(簡稱“周跑量”),得到如下的頻數分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人數 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答題卡上補全該市1000名跑步愛好者周跑量的頻率分布直方圖:

注:請先用鉛筆畫,確定后再用黑色水筆描黑
(2)根據以上圖表數據計算得樣本的平均數為![]() ,試求樣本的中位數(保留一位小數),并用平均數、中位數等數字特征估計該市跑步愛好者周跑量的分布特點
,試求樣本的中位數(保留一位小數),并用平均數、中位數等數字特征估計該市跑步愛好者周跑量的分布特點
(3)根據跑步愛好者的周跑量,將跑步愛好者分成以下三類,不同類別的跑者購買的裝備的價格不一樣,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
類別 | 休閑跑者 | 核心跑者 | 精英跑者 |
裝備價格(單位:元) | 2500 | 4000 | 4500 |
根據以上數據,估計該市每位跑步愛好者購買裝備,平均需要花費多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com