
【題目】如圖,直線![]() 與拋物線
與拋物線![]() (常數(shù)
(常數(shù)![]() )相交于不同的兩點
)相交于不同的兩點![]() 、
、![]() ,且
,且![]() (
(![]() 為定值),線段
為定值),線段![]() 的中點為
的中點為![]() ,與直線
,與直線![]() 平行的切線的切點為
平行的切線的切點為![]() (不與拋物線對稱軸平行或重合且與拋物線只有一個公共點的直線稱為拋物線的切線,這個公共點為切點).
(不與拋物線對稱軸平行或重合且與拋物線只有一個公共點的直線稱為拋物線的切線,這個公共點為切點).

(1)用![]() 、
、![]() 表示出
表示出![]() 點、
點、![]() 點的坐標(biāo),并證明
點的坐標(biāo),并證明![]() 垂直于
垂直于![]() 軸;
軸;
(2)求![]() 的面積,證明
的面積,證明![]() 的面積與
的面積與![]() 、
、![]() 無關(guān),只與
無關(guān),只與![]() 有關(guān);
有關(guān);
(3)小張所在的興趣小組完成上面兩個小題后,小張連![]() 、
、![]() ,再作與
,再作與![]() 、
、![]() 平行的切線,切點分別為
平行的切線,切點分別為![]() 、
、![]() ,小張馬上寫出了
,小張馬上寫出了![]() 、
、![]() 的面積,由此小張求出了直線
的面積,由此小張求出了直線![]() 與拋物線圍成的面積,你認(rèn)為小張能做到嗎?請你說出理由.
與拋物線圍成的面積,你認(rèn)為小張能做到嗎?請你說出理由.
【答案】(1)![]() ,
,![]() ,(2)
,(2)![]() ,(3)能.
,(3)能.
【解析】
試題(1)因為D點為直線與拋物線的交點A,B中點,所以求D點坐標(biāo)就根據(jù)直線方程與拋物線方程聯(lián)立方程組,利用韋達(dá)定理求解,即由![]() ,得
,得![]() ,
,![]() ,點
,點![]() .因為C點為切點,利用切線方程與拋物線方程聯(lián)立方程組后的判別式為零進(jìn)行求解,即由
.因為C點為切點,利用切線方程與拋物線方程聯(lián)立方程組后的判別式為零進(jìn)行求解,即由![]() ,得
,得![]() ,得
,得![]() .由于
.由于![]() 、
、![]() 的橫坐標(biāo)相同,
的橫坐標(biāo)相同,![]()
![]() 垂直于
垂直于![]() 軸.(2)求三角形面積,必須觀察結(jié)構(gòu),合理選用底邊與高.本題將CD選為底,則
軸.(2)求三角形面積,必須觀察結(jié)構(gòu),合理選用底邊與高.本題將CD選為底,則![]() 為高,利用(1)求出
為高,利用(1)求出![]() ,則
,則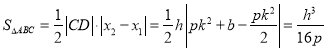 ,(3)對題目“馬上”的理解,就是進(jìn)行類比,直接寫出結(jié)論. 由(1)知
,(3)對題目“馬上”的理解,就是進(jìn)行類比,直接寫出結(jié)論. 由(1)知![]() 垂直于
垂直于![]() 軸,
軸,![]() ,由(2)可得
,由(2)可得![]() 、
、![]() 的面積只與
的面積只與![]() 有關(guān),將
有關(guān),將![]() 中的
中的![]() 換成
換成![]() ,可得
,可得![]() .而這一過程可無限類比下去,依次得到一列數(shù):
.而這一過程可無限類比下去,依次得到一列數(shù):![]() ,
,![]() ,這些數(shù)構(gòu)成一個公比為
,這些數(shù)構(gòu)成一個公比為![]() 無窮等比數(shù)列,其和可看成直線
無窮等比數(shù)列,其和可看成直線![]() 與拋物線圍成的面積,即
與拋物線圍成的面積,即![]()
試題解析:(1)由![]() ,得
,得![]() ,
,![]()
點![]() 2分
2分
設(shè)切線方程為![]() ,由
,由![]() ,得
,得![]() ,
,![]() ,切點的橫坐標(biāo)為
,切點的橫坐標(biāo)為![]() ,得
,得![]() 4分
4分
由于![]() 、
、![]() 的橫坐標(biāo)相同,
的橫坐標(biāo)相同,![]()
![]() 垂直于
垂直于![]() 軸. 6分
軸. 6分
(2)![]()
![]() ,
,![]()
![]() . 8分
. 8分
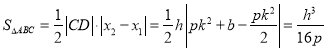 . 11分
. 11分
![]() 的面積與
的面積與![]() 、
、![]() 無關(guān),只與
無關(guān),只與![]() 有關(guān). 12分
有關(guān). 12分
(本小題也可以求![]() ,切點到直線
,切點到直線![]() 的距離
的距離 ,相應(yīng)給分)
,相應(yīng)給分)
(3)由(1)知![]() 垂直于
垂直于![]() 軸,
軸,![]() ,由(2)可得
,由(2)可得![]() 、
、![]() 的面積只與
的面積只與![]() 有關(guān),將
有關(guān),將![]() 中的
中的![]() 換成
換成![]() ,可得
,可得![]() . 14分
. 14分
記![]() ,
,![]() ,按上面構(gòu)造三角形的方法,無限的進(jìn)行下去,可以將拋物線
,按上面構(gòu)造三角形的方法,無限的進(jìn)行下去,可以將拋物線![]() 與線段
與線段![]() 所圍成的封閉圖形的面積,看成無窮多個三角形的面積的和,即數(shù)列
所圍成的封閉圖形的面積,看成無窮多個三角形的面積的和,即數(shù)列![]() 的無窮項和,此數(shù)列公比為
的無窮項和,此數(shù)列公比為![]() .
.


 寒假創(chuàng)新型自主學(xué)習(xí)第三學(xué)期寒假銜接系列答案
寒假創(chuàng)新型自主學(xué)習(xí)第三學(xué)期寒假銜接系列答案科目:高中數(shù)學(xué) 來源: 題型:
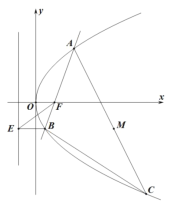
【題目】如圖,已知拋物線![]() 的焦點為
的焦點為![]() ,準(zhǔn)線為
,準(zhǔn)線為![]() ,過點
,過點![]() 的直線交拋物線于
的直線交拋物線于![]() ,
,![]() 兩點,點
兩點,點![]() 在準(zhǔn)線
在準(zhǔn)線![]() 上的投影為
上的投影為![]() ,點
,點![]() 是拋物線上一點,且滿足
是拋物線上一點,且滿足![]() .
.
(1)若點![]() 坐標(biāo)是
坐標(biāo)是![]() ,求線段
,求線段![]() 中點
中點![]() 的坐標(biāo);
的坐標(biāo);
(2)求![]() 面積的最小值及此時直線
面積的最小值及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱ABC-A1B1C1中,側(cè)面AA1C1C是矩形,平面ABC⊥平面AA1C1C,AB=2,AC=1,![]() ,
,![]() .
.
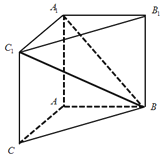
(1)求證:AA1⊥平面ABC;
(2)在線段BC1上是否存在一點D,使得AD⊥A1B?若存在求出![]() 的值,若不存在請說明理由.
的值,若不存在請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,CM,CN為某公園景觀湖胖的兩條木棧道,∠MCN=120°,現(xiàn)擬在兩條木棧道的A,B處設(shè)置觀景臺,記BC=a,AC=b,AB=c(單位:百米)
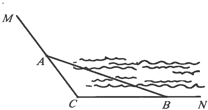
(1)若a,b,c成等差數(shù)列,且公差為4,求b的值;
(2)已知AB=12,記∠ABC=θ,試用θ表示觀景路線A-C-B的長,并求觀景路線A-C-B長的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標(biāo)原點
為參數(shù)),以坐標(biāo)原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標(biāo)系(
軸正半軸為極軸,建立極坐標(biāo)系(![]() ),點
),點![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 的延長線上,且滿足
的延長線上,且滿足![]() ,點
,點![]() 的軌跡為
的軌跡為![]() 。
。
(Ⅰ)求![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(Ⅱ)設(shè)點![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,求
,求![]() 面積的最小值。
面積的最小值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,從參加環(huán)保知識競賽的1200名學(xué)生中抽出![]() 名,將其成績(均為整數(shù))整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:
名,將其成績(均為整數(shù))整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:

(1)![]() 這一組的頻數(shù)、頻率分別是多少?
這一組的頻數(shù)、頻率分別是多少?
(2)估計這次環(huán)保知識競賽的及格率。(![]() 分及以上為及格)
分及以上為及格)
(3)若準(zhǔn)備取成績最好的300名發(fā)獎,則獲獎的最低分?jǐn)?shù)約為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在著名的漢諾塔問題中,有三根高度相同的柱子和一些大小及顏色各不相同的圓盤,三根柱子分別為起始柱、輔助柱及目標(biāo)柱.已知起始柱上套有![]() 個圓盤,較大的圓盤都在較小的圓盤下面.現(xiàn)把圓盤從起始柱全部移到目標(biāo)柱上,規(guī)則如下:每次只能移動一個圓盤,且每次移動后,每根柱上較大的圓盤不能放在較小的圓盤上面,規(guī)定一個圓盤從任一根柱上移動到另一根柱上為一次移動.若將
個圓盤,較大的圓盤都在較小的圓盤下面.現(xiàn)把圓盤從起始柱全部移到目標(biāo)柱上,規(guī)則如下:每次只能移動一個圓盤,且每次移動后,每根柱上較大的圓盤不能放在較小的圓盤上面,規(guī)定一個圓盤從任一根柱上移動到另一根柱上為一次移動.若將![]() 個圓盤從起始柱移動到目標(biāo)柱上最少需要移動的次數(shù)記為
個圓盤從起始柱移動到目標(biāo)柱上最少需要移動的次數(shù)記為![]() ,則
,則![]() ( )
( )

A. 33B. 31C. 17D. 15
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com