D
分析:根據題意,a可取的值為1、2、3、…25,由三角形的三邊關系,有25≤c<25+a,對a分情況討論,分析可得c可取的情況,即可得這種情況下符合條件的三角形的個數,由分類計數原理,結合等差數列的前n項和公式,計算可得答案.
解答:根據題意,a可取的值為1、2、3、…25,
根據三角形的三邊關系,有25≤c<25+a,
當a=1時,有25≤c<26,則c=25,有1種情況,
當a=2時,有25≤c<27,則c=25、26,有2種情況,
當a=3時,有25≤c<28,則c=25、26、27,有3種情況,
當a=4時,有25≤c<29,則c=25、26、27、28,有4種情況,
…
當a=25時,有有25≤c<50,則c=25、26、27、28…49,有25種情況,
則符合條件的三角形共有1+2+3+4+…+25=
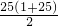
=325;
故選D.
點評:本題考查合情推理與分類計數原理的運用,涉及三角形三邊的關系,關鍵是發現a變化時,符合條件的三角形個數的變化規律.

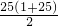 =325;
=325;
