
【題目】已知函數![]() ,
,![]() (
(![]() 是
是![]() 的導函數),
的導函數),![]() 在
在![]() 上的最大值為
上的最大值為![]() .
.
(1)求實數![]() 的值;
的值;
(2)判斷函數![]() 在
在![]() 內的極值點個數,并加以證明.
內的極值點個數,并加以證明.
【答案】(1)![]() (2)
(2)![]() 在
在![]() 上共有兩個極值點,詳見解析
上共有兩個極值點,詳見解析
【解析】
(1)先求得![]() ,再求得
,再求得![]() ,再討論
,再討論![]() 的符號,判斷函數
的符號,判斷函數![]() 的單調性,再求最值即可得解;
的單調性,再求最值即可得解;
(2)利用(1)的結論,結合![]() ,
,![]() ,由零點定理可
,由零點定理可![]() 在
在![]() 上有且僅有一個變號零點;再當
上有且僅有一個變號零點;再當![]() 時,由導數的應用可
時,由導數的應用可![]() 使
使![]() ,即
,即![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,再結合特殊變量所對應的函數值的符號可得
上單調遞減,再結合特殊變量所對應的函數值的符號可得![]() 在
在![]() 上有且僅有一個變號零點,綜合即可得解.
上有且僅有一個變號零點,綜合即可得解.
解:(1)由![]()
則![]() ,
,
則![]() ,
,
①當![]() 時
時![]() ,不合題意,舍去.
,不合題意,舍去.
②當![]() 時
時![]() ,∴
,∴![]() 在
在![]() 上單調遞減,∴
上單調遞減,∴![]() ,不合題意,舍去.
,不合題意,舍去.
③當![]() 時
時![]() ,∴
,∴![]() 在
在![]() 上單調遞增,∴
上單調遞增,∴![]() ,解得
,解得![]() ,
,
∴綜上:![]() .
.
(2)由(Ⅰ)知![]() ,
,![]() ,
,
當![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,
,![]() ,
,
∴![]() 在
在![]() 上有且僅有一個變號零點;
上有且僅有一個變號零點;
當![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上單調遞減.
上單調遞減.
又![]() ,
,![]() ,
,
∴![]() 使
使![]() 且當
且當![]() 時
時![]() ,當
,當![]() 時
時![]() ,
,
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
又![]() ,
,![]() ,
,![]() ,∴
,∴![]() 在
在![]() 上有且僅有一個變號零點.
上有且僅有一個變號零點.
∴![]() 在
在![]() 和
和![]() 上各有一個變號零點,∴
上各有一個變號零點,∴![]() 在
在![]() 上共有兩個極值點.
上共有兩個極值點.


科目:高中數學 來源: 題型:
【題目】眾所周知,城市公交車的數量太多會造成資源的浪費,太少又難以滿足乘客的需求,為此,某市公交公司在某站臺的50名候車乘客中隨機抽取10名,統計了他們的候車時間(單位:分鐘),得到下表.
候車時間 | 人數 |
| 1 |
| 4 |
| 2 |
| 2 |
| 1 |
(1)估計這10名乘客的平均候車時間(同一組中的每個數據可用該組區間的中點值代替);
(2)估計這50名乘客的候車時間少于10分鐘的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD的底面ABCD為正方形,![]() ,E,F分別是棱PC,AB的中點.
,E,F分別是棱PC,AB的中點.
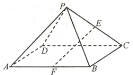
(1)求證:![]() 平面PAD;
平面PAD;
(2)若![]() ,求直線EF與平面PAB所成角的正弦值.
,求直線EF與平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
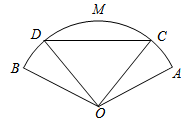
【題目】如圖,有一塊半徑為20米,圓心角![]() 的扇形展示臺,展示臺分成了四個區域:三角形
的扇形展示臺,展示臺分成了四個區域:三角形![]() ,弓形
,弓形![]() ,扇形
,扇形![]() 和扇形
和扇形![]() (其中
(其中![]() ).某次菊花展依次在這四個區域擺放:泥金香、紫龍臥雪、朱砂紅霜、朱砂紅霜.預計這三種菊花展示帶來的日效益分別是:泥金香50元/米
).某次菊花展依次在這四個區域擺放:泥金香、紫龍臥雪、朱砂紅霜、朱砂紅霜.預計這三種菊花展示帶來的日效益分別是:泥金香50元/米![]() ,紫龍臥雪30元/米
,紫龍臥雪30元/米![]() ,朱砂紅霜40元/米
,朱砂紅霜40元/米![]() .
.
(1)設![]() ,試建立日效益總量
,試建立日效益總量![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)試探求![]() 為何值時,日效益總量達到最大值.
為何值時,日效益總量達到最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某地區年齡在25~55歲的人員中,隨機抽出100人,了解他們對今年兩會的熱點問題的看法,繪制出頻率分布直方圖如圖所示,則下列說法正確的是( )

A. 抽出的100人中,年齡在40~45歲的人數大約為20
B. 抽出的100人中,年齡在35~45歲的人數大約為30
C. 抽出的100人中,年齡在40~50歲的人數大約為40
D. 抽出的100人中,年齡在35~50歲的人數大約為50
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現將甲、乙、丙、丁四個人安排到座位號分別是![]() 的四個座位上,他們分別有以下要求,
的四個座位上,他們分別有以下要求,
甲:我不坐座位號為![]() 和
和![]() 的座位;
的座位;
乙:我不坐座位號為![]() 和
和![]() 的座位;
的座位;
丙:我的要求和乙一樣;
丁:如果乙不坐座位號為![]() 的座位,我就不坐座位號為
的座位,我就不坐座位號為![]() 的座位.
的座位.
那么坐在座位號為![]() 的座位上的是( )
的座位上的是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com