Question

有一山坡，它與底面所成的二面角的大小是30°，山坡上有一條小路與坡腳線成45°角，某人沿此小路向上慢跑了200米，則他升高了

1. A.
   50米
2. B.
   50米
3. C.
   75米
4. D.
   100米

Answer 1

A
分析：畫出二面角α-L-β（二面角的大小是30°）在面α內過坡腳線畫一條斜線AB使得|AB|=200，再過B向β作垂線垂足為O過O做OC⊥L垂足為C連接BC則易得OB即為此人升高的高度然后利用三角形的有關知識求出OB的長度即可．
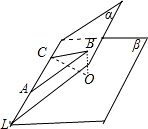
解答：解：如上圖|AB|=200且∠CAB=45°，過B向β作垂線垂足為O過O做OC⊥L垂足為C連接BC則易得OB即為此人升高的高度
∵BO⊥α，L⊆α
∴L⊥BO
∵OC⊥L，CO∩BO=O
∴L⊥面OBC
∴L⊥BC
∴∠BCO即為二面角α-L-β的平面角即∠BCO=30°，，
∵在RT△ACB中∠ACB=90°，∠CAB=45°，|AB|=200
∴|BC|=100
又在RT△COB中，∠COB=90°，∠BCO=30°
∴|OB|=|BC|=50（米）
即此人升高了50米．
故答案選A
點評：本題主要考查解三角形在實際生活中的應用．解題的關鍵是首先要正確做出符合條件的圖形，其次要明白二面角的平面角是怎么作出來的，最后再利用線面垂直的判定定理和性質定理求解三角形！