
【題目】已知:以點C(t, ![]() )(t∈R,t≠0)為圓心的圓與x軸交于點O,A,與y軸交于點O,B,其中O為原點.
)(t∈R,t≠0)為圓心的圓與x軸交于點O,A,與y軸交于點O,B,其中O為原點.
(1)當(dāng)t=2時,求圓C的方程;
(2)求證:△OAB的面積為定值;
(3)設(shè)直線y=﹣2x+4與圓C交于點M,N,若|OM|=|ON|,求圓C的方程.
【答案】
(1)解:當(dāng)t=2時,圓心為C(2,1),
∴圓C的方程為(x﹣2)2+(y﹣1)2=5;
(2)證明:由題設(shè)知,圓C的方程為(x﹣t)2+(y﹣ ![]() )2=t2+
)2=t2+ ![]() ,
,
化簡得x2﹣2tx+y2﹣ ![]() y=0.
y=0.
當(dāng)y=0時,x=0或2t,則A(2t,0);
當(dāng)x=0時,y=0或 ![]() ,則B(0,
,則B(0, ![]() ),
),
∴S△AOB= ![]() OAOB=
OAOB= ![]() |2t||
|2t|| ![]() |=4為定值.
|=4為定值.
(3)解:∵OM=ON,則原點O在MN的中垂線上,設(shè)MN的中點為H,則CH⊥MN,
∴C、H、O三點共線,KMN=﹣2,則直線OC的斜率k= ![]() ,
,
∴t=2或t=﹣2.
∴圓心為C(2,1)或C(﹣2,﹣1),
∴圓C的方程為(x﹣2)2+(y﹣1)2=5或(x+2)2+(y+1)2=5.
由于當(dāng)圓方程為(x+2)2+(y+1)2=5時,直線2x+y﹣4=0到圓心的距離d>r,
此時不滿足直線與圓相交,故舍去,
∴所求的圓C的方程為(x﹣2)2+(y﹣1)2=5.
【解析】(1)當(dāng)t=2時,圓心為C(2,1),即可得出圓C的方程;(2)求出半徑,寫出圓的方程,再解出A、B的坐標,表示出面積即可;(3)設(shè)MN的中點為H,則CH⊥MN,根據(jù)C、H、O三點共線,KMN=﹣2,由直線OC的斜率k= ![]() ,求得t的值,可得所求的圓C的方程.
,求得t的值,可得所求的圓C的方程.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導(dǎo)學(xué)與測試系列答案
導(dǎo)學(xué)與測試系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=Asin(ωx+φ)(ω>0,0<φ< ![]() )的部分圖象如圖所示.
)的部分圖象如圖所示. 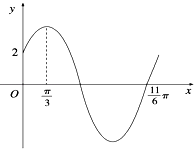
(1)求f(x)的解析式;
(2)將函數(shù)y=f(x)的圖象上所有點的縱坐標不變,橫坐標縮短為原來的 ![]() 倍,再將所得函數(shù)圖象向右平移
倍,再將所得函數(shù)圖象向右平移 ![]() 個單位,得到函數(shù)y=g(x)的圖象,求g(x)的單調(diào)遞增區(qū)間;
個單位,得到函數(shù)y=g(x)的圖象,求g(x)的單調(diào)遞增區(qū)間;
(3)當(dāng)x∈[﹣ ![]() ,
, ![]() ]時,求函數(shù)y=f(x+
]時,求函數(shù)y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() )的最值.
)的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖(1)所示,已知四邊形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且點
.且點![]() 為線段
為線段![]() 的中點,
的中點, ![]() ,
, ![]() 現(xiàn)將△
現(xiàn)將△![]() 沿
沿![]() 進行翻折,使得二面角
進行翻折,使得二面角![]()
![]() 的大小為
的大小為![]() ,得到圖形如圖(2)所示,連接
,得到圖形如圖(2)所示,連接![]() ,點
,點![]() 分別在線段
分別在線段![]() 上.
上.


(1)證明: ![]() ;
;
(2)若三棱錐![]() 的體積為四棱錐
的體積為四棱錐![]() 體積的
體積的![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() .
.
(Ⅰ)若![]() 在
在![]() 是單調(diào)遞增函數(shù),求實數(shù)
是單調(diào)遞增函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)令![]() ,若函數(shù)
,若函數(shù)![]() 有兩個零點,求實數(shù)
有兩個零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一個古典型(或幾何概型)中,若兩個不同隨機事件![]() 、
、![]() 概率相等,則稱
概率相等,則稱![]() 和
和![]() 是“等概率事件”,如:隨機拋擲一枚骰子一次,事件“點數(shù)為奇數(shù)”和“點數(shù)為偶數(shù)”是“等概率事件”,關(guān)于“等概率事件”,以下判斷正確的是__________.
是“等概率事件”,如:隨機拋擲一枚骰子一次,事件“點數(shù)為奇數(shù)”和“點數(shù)為偶數(shù)”是“等概率事件”,關(guān)于“等概率事件”,以下判斷正確的是__________.
①在同一個古典概型中,所有的基本事件之間都是“等概率事件”;
②若一個古典概型的事件總數(shù)為大于2的質(zhì)數(shù),則在這個古典概型中除基本事件外沒有其他“等概率事件”;③因為所有必然事件的概率都是1,所以任意兩個必然事件是“等概率事件”;
④隨機同時拋擲三枚硬幣一次,則事件“僅有一個正面”和“僅有兩個正面”是“等概率事件”.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(Ⅰ)若函數(shù)![]() 在
在![]() 處有極小值
處有極小值![]() ,求
,求![]() ,
,![]() 的值;
的值;
(Ⅱ)若![]() ,設(shè)
,設(shè)![]() ,求證:當(dāng)
,求證:當(dāng)![]() 時,
時,![]() ;
;
(Ⅲ)若![]() ,
,![]() ,對于給定
,對于給定![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,若
,若![]() .求
.求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的焦點在
的焦點在![]() 軸上,且橢圓
軸上,且橢圓![]() 的焦距為2.
的焦距為2.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,過
,過![]() 作
作![]() 軸且與橢圓
軸且與橢圓![]() 交于另一點
交于另一點![]() ,
, ![]() 為橢圓
為橢圓![]() 的右焦點,求證:三點
的右焦點,求證:三點![]() 在同一條直線上.
在同一條直線上.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】完成下列進位制之間的轉(zhuǎn)化.
(1)10231(4)=________(10);
(2)235(7)=________(10);
(3)137(10)=________(6);
(4)1231(5)=________(7);
(5)213(4)=________(3);
(6)1010111(2)=________(4).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com