
【題目】在長方體![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分別是所在棱
分別是所在棱![]() 、
、![]() 的中點,點
的中點,點![]() 是棱
是棱![]() 上的動點,聯結
上的動點,聯結![]() ,
,![]() .如圖所示.
.如圖所示.
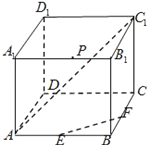
(1)求異面直線![]() ,
,![]() 所成角的大小(用反三角函數值表示);
所成角的大小(用反三角函數值表示);
(2)(理科)求以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的三棱錐的體積.
為頂點的三棱錐的體積.
(文科)求以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的三棱錐的體積.
為頂點的三棱錐的體積.
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,點
,點![]() 的極坐標為
的極坐標為![]() .
.
(1)求![]() 的直角坐標方程和
的直角坐標方程和![]() 的直角坐標;
的直角坐標;
(2)設![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】影響消費水平的原因很多,其中重要的一項是工資收入.研究這兩個變量的關系的一個方法是通過隨機抽樣的方法,在一定范圍內收集被調查者的工資收入和他們的消費狀況.下面的數據是某機構收集的某一年內上海、江蘇、浙江、安徽、福建五個地區的職工平均工資與城鎮居民消費水平(單位:萬元).
地區 | 上海 | 江蘇 | 浙江 | 安徽 | 福建 |
職工平均工資 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城鎮居民消費水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江蘇、浙江、安徽三個地區的職工平均工資和他們的消費水平,求出線性回歸方程![]() ,其中
,其中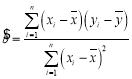
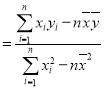 ,
,![]() ;
;
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過1萬,則認為得到的線性回歸方程是可靠的,試問所得的線性回歸方程是否可靠?(![]() 的結果保留兩位小數)
的結果保留兩位小數)
(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,其兩個頂點和兩個焦點構成的四邊形面積為
,其兩個頂點和兩個焦點構成的四邊形面積為![]() .
.
(1)求橢圓C的方程;
(2)過點![]() 的直線l與橢圓C交于A,B兩點,且點M恰為線段AB的中點,求直線l的方程.
的直線l與橢圓C交于A,B兩點,且點M恰為線段AB的中點,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,錯誤的是( )
A.圓錐所有的軸截面是全等的等腰三角形
B.圓柱的軸截面是過母線的截面中面積最大的一個
C.圓錐的軸截面是所有過頂點的界面中面積最大的一個
D.當球心到平面的距離小于球面半徑時,球面與平面的交線總是一個圓
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著社會的進步,經濟的發展,道路上的汽車越來越多,隨之而來的交通事故也增多.據有關部門調查,發生車禍的駕駛員中尤其是21 歲以下年輕人所占比例居高,因此交通管理有關部門,對2018 年參加駕照考試的21 歲以下學員隨機抽取10 名學員,對他們參加的科目三(道路駕駛)和科目四(安全文明駕駛相關知識)進行兩輪現場測試,并把兩輪測試成績的平均分作為該名學員的抽測成績.記錄的數據如下:
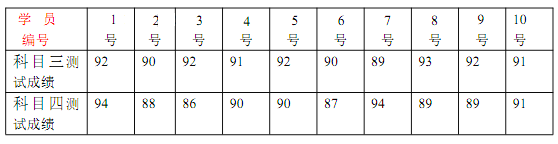
(1)從2018年參加駕照考試的21歲以下學員中隨機選取一名學員,試估計這名學員抽測成績大于或等于90分的概率;
(2)根據規定,科目三和科目四測試成績均達到90分以上(含90)才算測試合格.
(i)從抽測的1號至5號學員中任取兩名學員,記![]() 為學員測試合格的人數,求
為學員測試合格的人數,求![]() 的分布列和數學期望
的分布列和數學期望![]() ;
;
(ii) 記抽取的10名學員科目三和科目四測試成績的方差分別為![]() ,
,![]() ,試比較
,試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
某學校高一數學興趣小組對學生每周平均體育鍛煉小時數與體育成績優秀(體育成績滿分100分,不低于85分稱優秀)人數之間的關系進行分析研究,他們從本校初二,初三,高一,高二,高三年級各隨機抽取了40名學生,記錄并整理了這些學生周平均體育鍛煉小時數與體育成績優秀人數,得到如下數據表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均體育鍛煉小時數工(單位:小時) | 14 | 11 | 13 | 12 | 9 |
體育成績優秀人數y(單位:人) | 35 | 26 | 32 | 26 | 19 |
該興趣小組確定的研究方案是:先從這5組數據中選取3組數據求線性回歸方程,再用剩下的2組數據進行檢驗.
(1)若選取的是初三,高一,高二的3組數據,請根據這3組數據,求出y關于x的線性回歸方程![]() ;
;
(2)若由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差均不超過1,則認為得到的線性回歸方程是可靠的,試問(1)中所得到的線性回歸方程是否可靠?
參考數據:![]() ,
,![]() .
.
參考公式: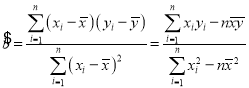 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com