解:(Ⅰ)∵定義在(0,+∞)上的函數f (x)對于任意的m,n∈(0,+∞),滿足f(m•n)=f(m)+f(n),
∴f(1)=f(1×1)=f(1)+f(1).∴f(1)=0
證明:(II)設0<x
1<x
2,∵f(m•n)=f(m)+f(n)即f(m•n)-f(m)=f(n)
∴
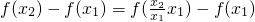
=
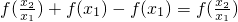
.
因為0<x
1<x
2,則

,而當x>1時,f(x)<0,從而f(x
2)<f(x
1)
于是f(x)在(0,+∞)上是減函數.
解:(Ⅲ)因為f(4)=f(2)+f(2)=-1,所以f(x
2-3x)>f(4),
因為f(x)在(0,+∞)上是減函數,所以0<x
2-3x<4,
解得-1<x<0或3<x<4,
故所求不等式的解集為{x|-1<x<0或3<x<4}.
分析:(Ⅰ)用賦值法求f(1)的值,因為定義在(0,+∞)上的函數f (x)對于任意的m,n∈(0,+∞),滿足f(m•n)=f(m)+f(n),所以只需令m=n=1,即可求出f(1)的值.
(Ⅱ)用函數單調性的定義證明,步驟是,先設所給區間上任意兩個自變量x
1,x
2,且x
1<x
2,再用作差法比較f(x
1),f(x
2)的大小,比較時,借助f(m•n)=f(m)+f(n),把x
2用

表示即可.
(Ⅲ)先根據
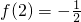
以及f(m•n)=f(m)+f(n)求出f(4)=-1,把不等式f(x
2-3x)>-1化為f(x
2-3x)>f(4),再利用(II)中判斷的函數的單調性解不等式即可.
點評:本題主要考查了賦值法求抽象函數的函數值,抽象函數的單調性的證明,以及借助函數單調性解不等式.

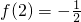 時,解不等式f(x2-3x)>-1.
時,解不等式f(x2-3x)>-1.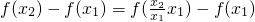 =
=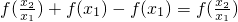 .
. ,而當x>1時,f(x)<0,從而f(x2)<f(x1)
,而當x>1時,f(x)<0,從而f(x2)<f(x1) 表示即可.
表示即可.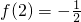 以及f(m•n)=f(m)+f(n)求出f(4)=-1,把不等式f(x2-3x)>-1化為f(x2-3x)>f(4),再利用(II)中判斷的函數的單調性解不等式即可.
以及f(m•n)=f(m)+f(n)求出f(4)=-1,把不等式f(x2-3x)>-1化為f(x2-3x)>f(4),再利用(II)中判斷的函數的單調性解不等式即可.

 閱讀快車系列答案
閱讀快車系列答案