
已知點(1, )是函數
)是函數 且
且 )的圖象上一點,等比數列
)的圖象上一點,等比數列 的前
的前 項和為
項和為 ,數列
,數列
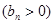 的首項為
的首項為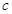 ,且前
,且前 項和
項和 滿足
滿足 -
- =
= +
+ (
( ).
).
(1)求數列 和
和 的通項公式;
的通項公式;
(2)求數列{ 前
前 項和為
項和為 .
.
(1)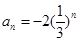 ,
,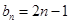 ;(2) 112.
;(2) 112.
【解析】
試題分析:(1)根據已知條件先求出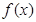 的表達式,這樣等比數列
的表達式,這樣等比數列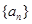 前
前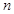 項和
項和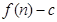 就清楚了,既然數列
就清楚了,既然數列 是等比數列,我們可以用特殊值
是等比數列,我們可以用特殊值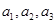 來求出參數
來求出參數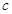 的值,從而求出
的值,從而求出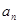 ,對數列
,對數列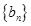 ,由前
,由前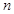 項和
項和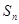 滿足
滿足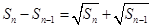 ,可變形為
,可變形為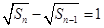 ,即數列
,即數列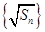 為等差數列,可以先求出
為等差數列,可以先求出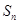 ,再求出
,再求出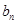 .(2)關鍵是求出和
.(2)關鍵是求出和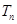 ,而數列{
,而數列{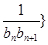 前
前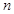 項和
項和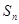 就可用裂項相消法求出,
就可用裂項相消法求出,
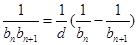 (
(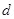 是數列
是數列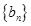 的公差}.
的公差}.
試題解析:(1)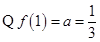 ,
,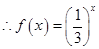
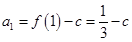 ,
,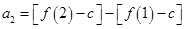
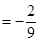 ,
,
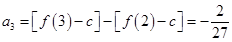 .
.
又數列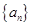 成等比數列,
成等比數列,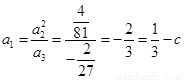 ,所以
,所以
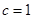 ;
;
又公比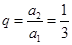 ,所以
,所以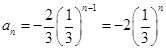
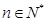 ; 3分
; 3分
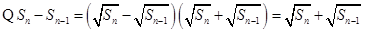
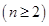
又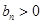 ,
,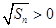 ,
,
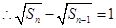 ;
;
數列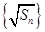 構成一個首相為1公差為1的等差數列,
構成一個首相為1公差為1的等差數列,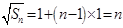 ,
,
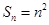
當 ,
,
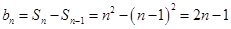 ;
;
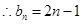 (
(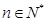 ); 7分
); 7分
(2)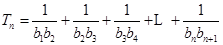
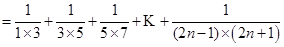

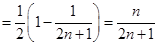 ; 12分
; 12分
考點:(1)①等比數列的定義;②由數列前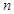 項和
項和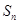 求數列通項;(2)裂項相消法求數列前
求數列通項;(2)裂項相消法求數列前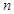 項和.
項和.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| 1 |
| 3 |
| Sn |
| Sn-1 |
| 1 |
| bnbn+1 |
| 1000 |
| 2011 |
| 2bn |
| a n |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省深圳市南頭中學高二(上)第一次考試數學試卷(解析版) 題型:解答題
 )是函數f(x)=ax(a>0),且a≠1)的圖象上一點,等比數列{an}的前n項和為f(n)-c,數列{bn}(bn>0)的首項為c,且前n項和Sn滿足Sn-Sn-1=
)是函數f(x)=ax(a>0),且a≠1)的圖象上一點,等比數列{an}的前n項和為f(n)-c,數列{bn}(bn>0)的首項為c,且前n項和Sn滿足Sn-Sn-1= +
+ (n≥2).
(n≥2). }前n項和為Tn,問Tn>
}前n項和為Tn,問Tn> 的最小正整數n是多少?
的最小正整數n是多少?查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建師大附中高三(上)期中數學試卷(文科)(解析版) 題型:解答題
 )是函數f(x)=ax(a>0),且a≠1)的圖象上一點,等比數列{an}的前n項和為f(n)-c,數列{bn}(bn>0)的首項為c,且前n項和Sn滿足Sn-Sn-1=
)是函數f(x)=ax(a>0),且a≠1)的圖象上一點,等比數列{an}的前n項和為f(n)-c,數列{bn}(bn>0)的首項為c,且前n項和Sn滿足Sn-Sn-1= +
+ (n≥2).
(n≥2). }前n項和為Tn,問Tn>
}前n項和為Tn,問Tn> 的最小正整數n是多少?
的最小正整數n是多少?查看答案和解析>>
科目:高中數學 來源:2013屆河南省商丘市高二第一學期第二次月考數學試卷 題型:解答題
(本題滿分12分) 已知點(1, )是函數
)是函數 且
且 )的圖象上一點,等比數列
)的圖象上一點,等比數列 的前
的前 項和為
項和為 ,數列
,數列
 的首項為
的首項為 ,且前
,且前 項和
項和 滿足
滿足 -
- =
= +
+ (
(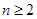 ).
).
(1)求數列 和
和 的通項公式;
的通項公式;
(2)若數列{ 前
前 項和為
項和為 ,問
,問 >
> 的最小正整數
的最小正整數 是多少?
是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com