
已知數(shù)列{bn}是等差數(shù)列,b1=1,b1+b2+…+b10=145。
(Ⅰ)求數(shù)列{bn}的能項bn;
(Ⅱ)設數(shù)列{an}的通項an=loga(1+1/bn)(其中a>0,且a≠1),記Sn是數(shù)列{an}的前n項的和。試比較Sn與1/3logabn+1的大小,并證明你的結論。
(Ⅰ)設數(shù)列![]() 的公差為
的公差為![]() ,由題意得
,由題意得
![]()
解得 ![]() ∴
∴![]()
(Ⅱ)由![]() ,知
,知
![]()
=![]()
因此要比較![]() 與
與![]() 的大小,可先比較
的大小,可先比較![]() 與
與![]() 的大小。
的大小。
取![]() 有
有![]() , 取
, 取![]() 有
有![]() , 由此推測
, 由此推測
![]()
若①式成立,則由對數(shù)函數(shù)性質可斷定: Sn>1/2lgbn+1。
下面用數(shù)學歸納法證明①式。
(i)當n=1時已驗證①式成立。
(ii)假設當n=k(k≥1)時,①式成立,即
![]()
那么,當n=k+1時,
![]() ∴
∴![]()
![]() /2k+1(2k+2)>
/2k+1(2k+2)> ![]() 。
。
因而(1+1)(1+1/3)…(1+1/2k-1)(1+1/2k+1) >![]()
這就是說①式當n=k+1時也成立。
由(i),(ii)知①式對任何正整數(shù)n都成立。
由此證得:Sn=1/2lgbn+1。


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| a | 2 n+1 |
| a | 2 n |
查看答案和解析>>
科目:高中數(shù)學 來源:2011年江蘇省南通市啟東中學高三考前輔導材料之小題強化篇1(解析版) 題型:解答題
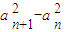 =d(其中d是常數(shù),n∈N﹡),則稱數(shù)列{an}是“等方差數(shù)列”.已知數(shù)列{bn}是公差為m的差數(shù)列,則m=0是“數(shù)列{bn}是等方差數(shù)列”的 條件.(填充分不必要、必要不充分、充要條件、既不充分也不必要條件中的一個)
=d(其中d是常數(shù),n∈N﹡),則稱數(shù)列{an}是“等方差數(shù)列”.已知數(shù)列{bn}是公差為m的差數(shù)列,則m=0是“數(shù)列{bn}是等方差數(shù)列”的 條件.(填充分不必要、必要不充分、充要條件、既不充分也不必要條件中的一個)查看答案和解析>>
科目:高中數(shù)學 來源:2011年江蘇省高考數(shù)學仿真押題試卷(02)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com