已知函數f（x）＝ex＋x，g（x）＝ln x＋x，h（x）＝ln x－1的零點依次為a，b，c，則（ ）
A．a＜b＜c B．c＜b＜a
C．c＜a＜b D．b＜a＜c
科學實驗活動冊系列答案科目：高中數學 來源：2013-2014學年河南省原名校高三上學期期聯考理科數學試卷（解析版） 題型：解答題
已知函數f（x）＝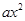
－（a＋2）x＋lnx.
（1）當a＝1時，求曲線y＝f（x）在點（1，f （1））處的切線方程；
（2）當a＞0時，若f（x）在區間[1，e）上的最小值為－2，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源：2012屆江西省上饒市高三第二次模擬考試理科數學試卷（解析版） 題型：解答題
（12分）已知函數f（x）＝lnx－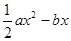
（a≠0）
（1）若a＝3，b＝－2，求f（x）在［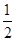
，e］的最大值；
（2）若b＝2，f（x）存在單調遞減區間，求a的范圍．
查看答案和解析>>
科目：高中數學 來源：2010-2011學年河南省五市高三第二次聯考理科數學 題型：解答題
（本小題滿分12分）
已知函數f（x）＝
－x （e為自然對數的底數）．
（Ⅰ）求f（x）的最小值；
（Ⅱ）不等式f（x）>ax的解集為P，若M＝{x｜
≤x≤2}且M∩P≠
，求實數a的
取值范圍；
（Ⅲ）已知n∈N﹡，且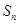
＝
（t為常數，t≥0），是否存在等比數列{
}，使得b1＋b2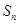＋…＝?若存在，請求出數列{}的通項公式；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源：2010年延安市高二下學期期末考試（理科）數學卷 題型：解答題
（本小題滿分14分）已知函數f（x）＝alnx＋x2（a為實常數）．
（Ⅰ）若a＝－2，求證：函數f（x）在（1，＋∞）上是增函數；
（Ⅱ）求函數f（x）在[1，e]上的最小值及相應的x值；
查看答案和解析>>
科目：高中數學 來源：2010年吉林省高二下學期期中考試數學（理） 題型：解答題
（本小題滿分12分）
已知函數f （x）＝alnx＋x2 （a為實常數）．[來源:ZXXK][來源:學*科*網Z*X*X*K]
（Ⅰ）若a＝－2，求證：函數f （x）在（1，＋∞）上是增函數；
（Ⅱ）求函數f （x）在[1，e]上的最小值及相應的x值；
（Ⅲ）若當x∈[1，e]時，f （x）≤（a＋2）x恒成立，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
