
【題目】已知函數f(x)= ![]() 為奇函數.
為奇函數.
(1)求實數m的值;
(2)用定義證明函數f(x)在區間(0,+∞)上為單調減函數;
(3)若關于x的不等式f(x)+a<0對區間[1,3]上的任意實數x都成立,求實數a的取值范圍.
【答案】
(1)∵f(﹣x)=﹣f(x),
∴ ![]() =﹣
=﹣ ![]() ,
,
解得:m=1
(2)證明:f(x)=1+ ![]() ,
,
設0<x1<x2,
∵f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
又1<2x1<2x2,2x1﹣1>0,2x2﹣1>0,x2﹣x1>0,
∴ ![]() >0,
>0,
∴f(x1)>f(x2),
∴函數f(x)在(0,+∞)遞減
(3)解:∵f(x)+a<0對區間[1,3]上的任意實數x都成立,
∴a<﹣f(x)對區間[1,3]上的任意實數x都成立,
∵f(x)在(0,+∞)遞減,
∴f(x)在[1,3]遞減,
∴f(x)的最大值是f(1)=3,
∴﹣f(x)的最小值是﹣3,
∴a<﹣3
【解析】(1)根據函數的奇偶性求出m的值即可;(2)根據函數單調性的定義證明即可;(3)問題轉化為a<﹣f(x)對區間[1,3]上的任意實數x都成立,求出f(x)的最大值,從而求出a的范圍即可.
【考點精析】關于本題考查的利用導數研究函數的單調性和函數的最大(小)值與導數,需要了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能得出正確答案.
比較,其中最大的是一個最大值,最小的是最小值才能得出正確答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,某市準備在道路EF的一側修建一條運動比賽道,賽道的前一部分為曲線段FBC,該曲線段是函數 ![]() (A>0,ω>0),x∈[﹣4,0]時的圖象,且圖象的最高點為B(﹣1,2).賽道的中間部分為長
(A>0,ω>0),x∈[﹣4,0]時的圖象,且圖象的最高點為B(﹣1,2).賽道的中間部分為長 ![]() 千米的直線跑道CD,且CD∥EF.賽道的后一部分是以O為圓心的一段圓弧
千米的直線跑道CD,且CD∥EF.賽道的后一部分是以O為圓心的一段圓弧 ![]() .
. 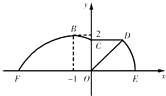
(1)求ω的值和∠DOE的大小;
(2)若要在圓弧賽道所對應的扇形ODE區域內建一個“矩形草坪”,矩形的一邊在道路EF上,一個頂點在半徑OD上,另外一個頂點P在圓弧 ![]() 上,且∠POE=θ,求當“矩形草坪”的面積取最大值時θ的值.
上,且∠POE=θ,求當“矩形草坪”的面積取最大值時θ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線l1:y=x,l2:y=x+2與圓C:x2+y2﹣2mx﹣2ny=0的四個交點把圓C分成的四條弧長相等,則m=( )
A.0或1
B.0或﹣1
C.1或﹣1
D.0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cosλθ,cos(10﹣λ)θ),
=(cosλθ,cos(10﹣λ)θ), ![]() =(sin(10﹣λ)θ,sinλθ),λ、θ∈R.
=(sin(10﹣λ)θ,sinλθ),λ、θ∈R.
(1)求 ![]() +
+ ![]() 的值;
的值;
(2)若 ![]() ⊥
⊥ ![]() ,求θ;
,求θ;
(3)若θ= ![]() ,求證:
,求證: ![]() ∥
∥ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,2)為圓C:x2+y2﹣2ax﹣2ay=0(a>0)外一點,圓C上存在點P使得∠CAP=45°,則實數a的取值范圍是( )
A.(0,1)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() ,
, ![]() .
.
(1)當n=1,2,3時,分別比較f(n)與g(n)的大小(直接給出結論);
(2)由(1)猜想f(n)與g(n)的大小關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公差為正數的等差數列,其前
是公差為正數的等差數列,其前![]() 項和為
項和為![]() ,且
,且![]() ,
, ![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)數列![]() 滿足
滿足![]() ,
, ![]() .①求數列
.①求數列![]() 的通項公式;②是否存在正整數
的通項公式;②是否存在正整數![]() ,
, ![]() (
(![]() ),使得
),使得![]() ,
, ![]() ,
, ![]() 成等差數列?若存在,求出
成等差數列?若存在,求出![]() ,
, ![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,兩個焦點分別為
,兩個焦點分別為![]() ,
, ![]() ,四邊形
,四邊形![]() 的面積是四邊形
的面積是四邊形![]() 的面積的2倍.
的面積的2倍.
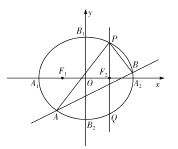
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的右焦點且垂直于
的右焦點且垂直于![]() 軸的直線交橢圓
軸的直線交橢圓![]() 于
于![]() 兩點,
兩點, ![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的兩點.若直線
兩側的兩點.若直線![]() 過點
過點![]() ,且
,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com