
【題目】為響應“精確扶貧”號召,某企業計劃每年用不超過100萬元的資金購買單價分別為1500元/箱和3000元/箱的A、B兩種藥品捐獻給貧困地區某醫院,其中A藥品至少100箱,B藥品箱數不少于A藥品箱數.則該企業捐獻給醫院的兩種藥品總箱數最多可為( )
A.200
B.350
C.400
D.500
 互動課堂系列答案
互動課堂系列答案 激活思維智能訓練課時導學練系列答案
激活思維智能訓練課時導學練系列答案科目:高中數學 來源: 題型:
【題目】已知點P與兩個定點O(0,0),A(-3,0)距離之比為![]() .
.
(1)求點P的軌跡C方程;
(2)求過點M(2,3)且被軌跡C截得的線段長為2![]() 的直線方程.
的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某知名品牌汽車深受消費者喜愛,但價格昂貴.某汽車經銷商推出A、B、C三種分期付款方式銷售該品牌汽車,并對近期100位采用上述分期付款的客戶進行統計分析,得到如下的柱狀圖.已知從A、B、C三種分期付款銷售中,該經銷商每銷售此品牌汽車1倆所獲得的利潤分別是1萬元,2萬元,3萬元.現甲乙兩人從該汽車經銷商處,采用上述分期付款方式各購買此品牌汽車一輛.以這100位客戶所采用的分期付款方式的頻率代替1位客戶采用相應分期付款方式的概率. 
(1)求甲乙兩人采用不同分期付款方式的概率;
(2)記X(單位:萬元)為該汽車經銷商從甲乙兩人購車中所獲得的利潤,求X的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,g(x)=lnx,其中e為自然對數的底數.
,g(x)=lnx,其中e為自然對數的底數.
(1)求函數y=f(x)g(x)在x=1處的切線方程;
(2)若存在x1 , x2(x1≠x2),使得g(x1)﹣g(x2)=λ[f(x2)﹣f(x1)]成立,其中λ為常數,求證:λ>e;
(3)若對任意的x∈(0,1],不等式f(x)g(x)≤a(x﹣1)恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校的平面示意圖為如下圖五邊形區域ABCDE,其中三角形區域ABE為生活區,四邊形區域BCDE為教學區,AB,BC,CD,DE,EA,BE為學校的主要道路(不考慮寬度). ![]() ,
, ![]() .
. 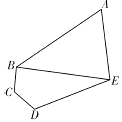
(1)求道路BE的長度;
(2)求生活區△ABE面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(x+a)﹣x,a∈R.
(1)當a=﹣1時,求f(x)的單調區間;
(2)若x≥1時,不等式ef(x)+ ![]() x2>1恒成立,求實數a的取值范圍.
x2>1恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣2a|+|x+ ![]() |
|
(1)當a=1時,求不等式f(x)>4的解集;
(2)若不等式f(x)≥m2﹣m+2 ![]() 對任意實數x及a恒成立,求實數m的取值范圍.
對任意實數x及a恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com