
設二次函數![]() 滿足下列兩個條件:
滿足下列兩個條件:
①當![]() 時,
時,![]() 的最小值為0,且
的最小值為0,且![]() 成立;
成立;
②當![]() 時,
時,![]() ≤
≤![]() 恒成立.
恒成立.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)求最大的實數![]() (
(![]() ),使得存在實數
),使得存在實數![]() ,當
,當![]() 時,有
時,有![]() 恒成立.
恒成立.
(1) ![]() (2)
(2) ![]()
(3) 存在t=-4 ,對任意的x∈[1,9] 恒有g(x)≤0, ∴m的最大值為9
(1)在②中令![]() ,有
,有![]() ,故
,故![]() …………………….3分
…………………….3分
(2)由①知二次函數的關于直線![]() 對稱,且開口向上………..4分
對稱,且開口向上………..4分
故設此二次函數為![]() ,(
,(![]() ),…………………6分
),…………………6分
∵![]() ,∴
,∴![]() ……………………………………….……….7分
……………………………………….……….7分
∴![]() ………………………………………………….8分
………………………………………………….8分
(3)假設存在![]() ,只需
,只需![]() ,就有
,就有![]() .
.
則![]()
![]()
![]() (x+t+1)2≤x
(x+t+1)2≤x![]() x2+(2t-2)x+t2+2t+1≤0…….10分
x2+(2t-2)x+t2+2t+1≤0…….10分
令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m]
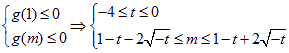 ………………………..12分
………………………..12分
∴m≤1-t+2![]() ≤1-(-4)+2
≤1-(-4)+2![]() =9
=9
即存在t=-4 ,對任意的x∈[1,9] 恒有g(x)≤0, ∴m的最大值為9……14分


科目:高中數學 來源: 題型:
| 2 |
| π |
| 6 |
| π |
| 4 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
| 2 |
| π |
| 6 |
| π |
| 4 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京大學附中高三(上)數學練習試卷5(文科)(解析版) 題型:填空題
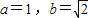 ,
,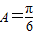 則
則 ;③設二次函數f(x)=x2+ax+a,則“
;③設二次函數f(x)=x2+ax+a,則“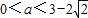 ”是“方程f(x)-x=0的兩根x1和x2滿足0<x1<x2<1”的充分必要條件.④過點(
”是“方程f(x)-x=0的兩根x1和x2滿足0<x1<x2<1”的充分必要條件.④過點( ,1)且與函數y=
,1)且與函數y=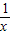 的圖象相切的直線方程是4x+y-3=0.其中所有正確說法的序號是 .
的圖象相切的直線方程是4x+y-3=0.其中所有正確說法的序號是 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com