
【題目】已知等差數列![]() 的前
的前![]() 項的和為
項的和為![]() ,公差
,公差![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比數列,
成等比數列,![]() ;數列
;數列![]() 滿足:對于任意的
滿足:對于任意的![]() ,等式
,等式![]() 都成立.
都成立.
(1)求數列![]() 的通項公式;
的通項公式;
(2)證明:數列![]() 是等比數列;
是等比數列;
(3)若數列![]() 滿足
滿足![]() ,試問是否存在正整數
,試問是否存在正整數![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比數列?若存在,求出所有滿足條件的數組
成等比數列?若存在,求出所有滿足條件的數組![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
【答案】(1) ![]() ;(2)見解析;(3)見解析.
;(2)見解析;(3)見解析.
【解析】分析:(1)根據已知解方程組得![]() ,即得數列
,即得數列![]() 的通項公式.(2)利用作差法化簡
的通項公式.(2)利用作差法化簡
![]() 即得
即得![]() ,即證明數列
,即證明數列![]() 是等比數列.(3)先化簡
是等比數列.(3)先化簡![]() ,再化簡
,再化簡![]() ,
,![]() ,
,![]() 成等比數列,對s分類討論得解.
成等比數列,對s分類討論得解.
詳解:(1)設數列![]() 公差為
公差為![]() ,由題設得
,由題設得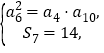
即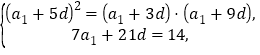 解得
解得![]()
∴數列![]() 的通項公式為:
的通項公式為:![]() .
.
(2)∵![]()
∴![]() ,①
,①
∴![]() ,②
,②
由②-①得![]() ,③
,③
∴![]() ,④
,④
由④-③得![]() ,
,
由①知![]() ,
,![]() ,∴
,∴![]() .
.
又![]() ,∴數列
,∴數列![]() 是等比數列.
是等比數列.
(3)假設存在正整數![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比數列,則
成等比數列,則![]() ,
,![]() ,
,![]() 成等差數列.
成等差數列.
由(2)可知:![]() ,∴
,∴![]() .
.
于是,![]() .
.
由于![]() ,所以
,所以![]()
因為當![]() 時,
時,![]() ,即
,即![]() 單調遞減,
單調遞減,
所以當![]() 時,
時,![]() ,不符合條件,
,不符合條件,
所以![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]()
當![]() 時,得
時,得![]() ,無解,
,無解,
當![]() 時,得
時,得![]() ,所以
,所以![]() ,
,
綜上:存在唯一正整數數組![]() ,使
,使![]() ,
,![]() ,
,![]() 成等比數列.
成等比數列.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分別為角A,B,C的對邊,在四面體PABC中,S1,S2,S3,S分別表示△PAB,△PBC,△PCA,△ABC的面積,α,β,γ依次表示面PAB,面PBC,面PCA與底面ABC所成二面角的大小.寫出對四面體性質的猜想,并證明你的結論


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知任意角
中,已知任意角![]() 以坐標原點
以坐標原點![]() 為頂點,
為頂點,![]() 軸的非負半軸為始邊,若終邊經過點
軸的非負半軸為始邊,若終邊經過點![]() ,且
,且![]() ,定義:
,定義:![]() ,稱“
,稱“![]() ”為“正余弦函數”,對于“正余弦函數
”為“正余弦函數”,對于“正余弦函數![]() ”,有同學得到以下性質:
”,有同學得到以下性質:
①該函數的值域為![]() ; ②該函數的圖象關于原點對稱;
; ②該函數的圖象關于原點對稱;
③該函數的圖象關于直線![]() 對稱; ④該函數為周期函數,且最小正周期為
對稱; ④該函數為周期函數,且最小正周期為![]() ;
;
⑤該函數的遞增區間為![]() .
.
其中正確的是__________.(填上所有正確性質的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為實常數) .
為實常數) .
(I)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值及相應的
上的最大值及相應的![]() 值;
值;
(II)當![]() 時,討論方程
時,討論方程![]() 根的個數.
根的個數.
(III)若![]() ,且對任意的
,且對任意的![]() ,都有
,都有 ,求
,求
實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解用戶對其產品的滿意度,從A,B兩地區分別隨機調查了40個用戶,根據用戶對產品的滿意度評分,得到A地區用戶滿意度評分的頻率分布直方圖和B地區用戶滿意度評分的頻數分布表。
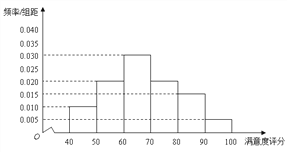
A地區用戶滿意度評分的頻率分布直方圖

B地區用戶滿意度評分的頻數分布表
(Ⅰ)在答題卡上作出B地區用戶滿意度評分的頻率分布直方圖,并通過直方圖比較兩地區滿意度評分的平均值及分散程度(不要求計算出具體值,給出結論即可);
(Ⅱ)根據用戶滿意度評分,將用戶的滿意度從低到高分為三個等級:
滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
估計哪個地區的滿意度等級為不滿意的概率大?說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 中,
中, ![]() =
= ![]() =
=![]() =
= ![]() 分別在
分別在![]() 上,
上, ![]() ,現將四邊形
,現將四邊形![]() 沿
沿![]() 折起,使
折起,使![]() .
.

(1)若![]() ,在折疊后的線段
,在折疊后的線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(2)求三棱錐![]() 的體積的最大值,并求出此時點
的體積的最大值,并求出此時點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,函數
,函數![]() 的最小值為
的最小值為![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)求![]() ;
;
(3)已知函數![]() 為定義在上的增函數,且對任意的
為定義在上的增函數,且對任意的![]() 都滿足
都滿足![]() ,問:是否存在這樣的實數
,問:是否存在這樣的實數![]() ,使不等式
,使不等式![]() 對所有
對所有![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com