解:(1)∵f(x)=x
3-
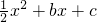
,
∴f′(x)=3x
2-x+b,….(1分)
∵f(x)在x=1處取極值,
∴f′(1)=0 …(2分)
∴3-1+b=0
即b=-2 …(3分)
(2)由(1)可得f′(x)=3x
2-x-2
令f′(x)=0,則x=

,或x=1 …..(4分)
∵x∈(-∞,

)時(shí),f′(x)>0,f(x)單調(diào)遞增;
當(dāng)x∈(

,1)時(shí),f′(x)<0,f(x)單調(diào)遞減;
當(dāng)x∈(1,+∞)時(shí),f′(x)>0,f(x)單調(diào)遞增.
∴在閉區(qū)間[-1,2]上,f(x)單調(diào)遞增 …(5分)
∴在閉區(qū)間[-1,2]上,f(x)的最大值為f(2)=2+c<c
2,…(6分)
∴c>2,或c<-1 …(7分)
(3)由(1)、(2)可知:
f(x)的極大值為f(

)=
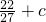
,
f(x)的極小值為f(1)=c-

…(8分)
∵當(dāng)f(

)<0,或f(1)>0時(shí),曲線y=f(x)與x軸僅有一個(gè)交點(diǎn) ….(9分)
∴
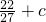
<0,或c-

>0,
即c<
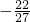
,或c>

時(shí),
曲線y=f(x)與x軸僅有一個(gè)交點(diǎn)…(10分)
分析:(1)由已知中函數(shù)f(x)=x
3-
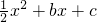
,且f(x)在x=1處取得極值,我們求出f′(x)的解析式,根據(jù)f′(1)=0,我們易可構(gòu)造一個(gè)關(guān)于b的方程,解方程即可得到b的值;
(2)利用導(dǎo)數(shù)法,我們可以判斷出當(dāng)x∈[1,2]時(shí),函數(shù)f(x)的單調(diào)性,進(jìn)而求出f(x)在區(qū)間[1,2]的最大值,根據(jù)當(dāng)x∈[1,2]時(shí),f(x)<c
2恒成立,可以構(gòu)造一個(gè)關(guān)于c的不等式,解不等式即可得到c的取值范圍;
(3)若曲線y=f(x)與x軸僅有一個(gè)交點(diǎn),則y=f(x)的極大值小于0,或y=f(x)的極小值大于0,進(jìn)而構(gòu)造關(guān)于x的不等式,解不等式即可求出c的取值范圍.
點(diǎn)評(píng):本題考查的知識(shí)點(diǎn)是利用導(dǎo)數(shù)求閉區(qū)間上函數(shù)的最值,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,其中根據(jù)函數(shù)的解析式,求出導(dǎo)函數(shù)的解析式是解答本題的關(guān)鍵.

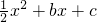 ,且f(x)在x=1處取得極值.
,且f(x)在x=1處取得極值.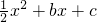 ,
, ,或x=1 …..(4分)
,或x=1 …..(4分) )時(shí),f′(x)>0,f(x)單調(diào)遞增;
)時(shí),f′(x)>0,f(x)單調(diào)遞增; ,1)時(shí),f′(x)<0,f(x)單調(diào)遞減;
,1)時(shí),f′(x)<0,f(x)單調(diào)遞減; )=
)=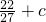 ,
, …(8分)
…(8分) )<0,或f(1)>0時(shí),曲線y=f(x)與x軸僅有一個(gè)交點(diǎn) ….(9分)
)<0,或f(1)>0時(shí),曲線y=f(x)與x軸僅有一個(gè)交點(diǎn) ….(9分)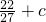 <0,或c-
<0,或c- >0,
>0,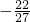 ,或c>
,或c> 時(shí),
時(shí),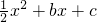 ,且f(x)在x=1處取得極值,我們求出f′(x)的解析式,根據(jù)f′(1)=0,我們易可構(gòu)造一個(gè)關(guān)于b的方程,解方程即可得到b的值;
,且f(x)在x=1處取得極值,我們求出f′(x)的解析式,根據(jù)f′(1)=0,我們易可構(gòu)造一個(gè)關(guān)于b的方程,解方程即可得到b的值;

 期末好成績(jī)系列答案
期末好成績(jī)系列答案 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百?gòu)?qiáng)名校期末沖刺100分系列答案
百?gòu)?qiáng)名校期末沖刺100分系列答案 好成績(jī)1加1期末沖刺100分系列答案
好成績(jī)1加1期末沖刺100分系列答案 金狀元績(jī)優(yōu)好卷系列答案
金狀元績(jī)優(yōu)好卷系列答案
 已知函數(shù)f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數(shù)f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<