
【題目】已知數列{an}的首項a1=a,其前n項和為Sn , 且滿足Sn+Sn﹣1=3n2+2n+4(n≥2),若對任意的n∈N* , an<an+1恒成立,則a的取值范圍是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(﹣∞, ![]() )
)
【答案】C
【解析】解:由Sn+Sn﹣1=3n2+2n+4(n≥2),可以得到Sn+1+Sn=3(n+1)2+2(n+1)+4, 兩式相減得an+1+an=6n+5,
故an+2+an+1=6n+11,兩式再相減得an+2﹣an=6,
由n=2得a1+a2+a1=20,a2=20﹣2a,
故偶數項為以20﹣2a為首項,以6為公差的等差數列,
從而a2n=6n+14﹣2a;
n=3得a1+a2+a3+a1+a2=37,a3=2a﹣3,
從而a2n+1=6n﹣9+2a,
由條件得 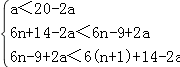 ,
,
解得 ![]() <a<
<a< ![]() ,
,
故選:C.
【考點精析】本題主要考查了數列的通項公式的相關知識點,需要掌握如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式才能正確解答此題.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
在如圖所示的多面體中,四邊形![]() 和
和![]() 都為矩形。
都為矩形。

(Ⅰ)若![]() ,證明:直線
,證明:直線![]() 平面
平面![]() ;
;
(Ⅱ)設![]() ,
, ![]() 分別是線段
分別是線段![]() ,
, ![]() 的中點,在線段
的中點,在線段![]() 上是否存在一點
上是否存在一點![]() ,使直線
,使直線![]() 平面
平面![]() ?請證明你的結論。
?請證明你的結論。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
已知函數![]() (
(![]() ),記
),記![]() 的導函數為
的導函數為![]() .
.
(1)證明:當![]() 時,
時,![]() 在
在![]() 上單調遞增;
上單調遞增;
(2)若![]() 在
在![]() 處取得極小值,求
處取得極小值,求![]() 的取值范圍;
的取值范圍;
(3)設函數![]() 的定義域為
的定義域為![]() ,區間
,區間![]() ,若
,若![]() 在
在![]() 上是單調函數,
上是單調函數,
則稱![]() 在
在![]() 上廣義單調.試證明函數
上廣義單調.試證明函數![]() 在
在![]() 上廣義單調.
上廣義單調.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(1+sin2x,sinx﹣cosx),
=(1+sin2x,sinx﹣cosx), ![]() =(1,sinx+cosx),函數f(x)=
=(1,sinx+cosx),函數f(x)= ![]()
(1)求函數f(x)的最小正周期;
(2)求函數f(x)的最大值及取得最大值相應的x的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某算法的程序框圖如圖所示,其中輸入的變量x在1,2,3,…,24這24個整數中等可能隨機產生. 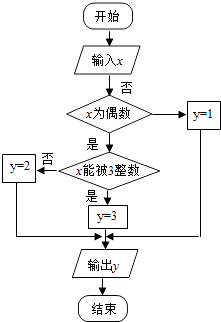
(1)分別求出按程序框圖正確編程運行時輸出y的值為i的概率Pi(i=1,2,3);
(2)甲、乙兩同學依據自己對程序框圖的理解,各自編寫程序重復運行n次后,統計記錄了輸出y的值為i(i=1,2,3)的頻數.以下是甲、乙所作頻數統計表的部分數據.
甲的頻數統計表(部分)
運行 | 輸出y的值 | 輸出y的值 | 輸出y的值 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的頻數統計表(部分)
運行 | 輸出y的值 | 輸出y的值 | 輸出y的值 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
當n=2100時,根據表中的數據,分別寫出甲、乙所編程序各自輸出y的值為i(i=1,2,3)的頻率(用分數表示),并判斷兩位同學中哪一位所編寫程序符合算法要求的可能性較大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com