
【題目】設fk(n)為關于n的k(k∈N)次多項式.數列{an}的首項a1=1,前n項和為Sn . 對于任意的正整數n,an+Sn=fk(n)都成立. (Ⅰ)若k=0,求證:數列{an}是等比數列;
(Ⅱ)試確定所有的自然數k,使得數列{an}能成等差數列.
【答案】解:(Ⅰ)證明:若k=0,則fk(n)即f0(n)為常數, 不妨設f0(n)=c(c為常數).
因為an+Sn=fk(n)恒成立,所以a1+S1=c,c=2a1=2.
而且當n≥2時,
an+Sn=2,①
an﹣1+Sn﹣1=2,②
①﹣②得 2an﹣an﹣1=0(n∈N,n≥2).
若an=0,則an﹣1=0,…,a1=0,與已知矛盾,所以an≠0(n∈N*).
故數列{an}是首項為1,公比為 ![]() 的等比數列.
的等比數列.
(Ⅱ)解:(1)若k=0,由(Ⅰ)知,不符題意,舍去.
⑵若k=1,設f1(n)=bn+c(b,c為常數),
當n≥2時,an+Sn=bn+c,③
an﹣1+Sn﹣1=b(n﹣1)+c,④
③﹣④得 2an﹣an﹣1=b(n∈N,n≥2).
要使數列{an}是公差為d(d為常數)的等差數列,
必須有an=b﹣d(常數),
而a1=1,故{an}只能是常數數列,通項公式為an=1(n∈N*),
故當k=1時,數列{an}能成等差數列,其通項公式為an=1(n∈N*),
此時f1(n)=n+1.
⑶若k=2,設f2(n)=pn2+qn+t(a≠0,a,b,c是常數),
當n≥2時,
an+Sn=pn2+qn+t,⑤
an﹣1+Sn﹣1=p(n﹣1)2+q(n﹣1)+t,⑥
⑤﹣⑥得 2an﹣an﹣1=2pn+q﹣p(n∈N,n≥2),
要使數列{an}是公差為d(d為常數)的等差數列,
必須有an=2pn+q﹣p﹣d,且d=2p,
考慮到a1=1,所以an=1+(n﹣1)2p=2pn﹣2p+1(n∈N*).
故當k=2時,數列{an}能成等差數列,
其通項公式為an=2pn﹣2p+1(n∈N*),
此時f2(n)=an2+(a+1)n+1﹣2a(a為非零常數).
⑷當k≥3時,若數列{an}能成等差數列,根據等差數列通項公式可知Sn是關于n的二次型函數,
則an+Sn的表達式中n的最高次數為2,
故數列{an}不能成等差數列.
綜上得,當且僅當k=1或2時,數列{an}能成等差數列
【解析】(Ⅰ)若k=0,不妨設f0(n)=c(c為常數).即an+Sn=c,結合數列中an與 Sn關系 ![]() 求出數列{an}的通項公式后再證明.(Ⅱ)由特殊到一般,實質上是由已知an+Sn=fk(n) 考查數列通項公式求解,以及等差數列的判定.
求出數列{an}的通項公式后再證明.(Ⅱ)由特殊到一般,實質上是由已知an+Sn=fk(n) 考查數列通項公式求解,以及等差數列的判定.
【考點精析】本題主要考查了等差關系的確定和等比關系的確定的相關知識點,需要掌握如果一個數列從第2項起,每一項與它的前一項的差等于同一個常數,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么這個數列就叫做等差數列;等比數列可以通過定義法、中項法、通項公式法、前n項和法進行判斷才能正確解答此題.
)那么這個數列就叫做等差數列;等比數列可以通過定義法、中項法、通項公式法、前n項和法進行判斷才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
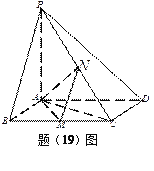
如圖,已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形,![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
, ![]() 分別是
分別是![]() 的中點。
的中點。
(1)證明: ![]() ;
;
(2)若![]() 為
為![]() 上的動點,
上的動點,![]() 與平面
與平面![]() 所成最大角
所成最大角
的正切值為![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的焦距為2,離心率為
的焦距為2,離心率為![]() ,
,![]() 軸上一點
軸上一點![]() 的坐標為
的坐標為![]() .
.
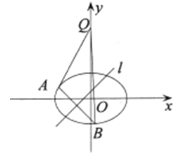
(Ⅰ)求該橢圓的方程;
(Ⅱ)若對于直線![]() ,橢圓
,橢圓![]() 上總存在不同的兩點
上總存在不同的兩點![]() 與
與![]() 關于直線
關于直線![]() 對稱,且
對稱,且![]() ,求
,求
實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且滿足a1= ![]() ,2Sn﹣SnSn﹣1=1(n≥2).
,2Sn﹣SnSn﹣1=1(n≥2).
(1)猜想Sn的表達式,并用數學歸納法證明;
(2)設bn= ![]() ,n∈N* , 求bn的最大值.
,n∈N* , 求bn的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了估計某人的射擊技術情況,在他的訓練記錄中抽取50次檢驗,他的命中環數如下:10,5,5,8,7,8,6,9,7,8,6,6,5,6,7,8,10,9,7,9,8,7,6,5,9,9,8,8,5,8,6,7,6,9,6,8,8,8,6,7,6,8,107,10,8,7,7,9,5
(1)列出頻率分布表
(2)畫出頻率分布的直方圖.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接黨的“十九”大的召開,某校組織了“歌頌祖國,緊跟黨走”黨史知識競賽,從參加考試的學生中抽出50名學生,將其成績(滿分100分,成績均為整數)分成六段![]() ,
, ![]() ,…,
,…, ![]() 后繪制頻率分布直方圖(如下圖所示)
后繪制頻率分布直方圖(如下圖所示)
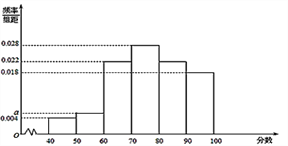
(Ⅰ)求頻率分布圖中![]() 的值;
的值;
(Ⅱ)估計參加考試的學生得分不低于80的概率;
(Ⅲ)從這50名學生中,隨機抽取得分在![]() 的學生2人,求此2人得分都在
的學生2人,求此2人得分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com