
【題目】已知公比不為1的等比數列{an}的前3項積為27,且2a2為3a1和a3的等差中項.
(1)求數列{an}的通項公式an;
(2)若數列{bn}滿足bn=bn﹣1log3an+1(n≥2,n∈N*),且b1=1,求數列{ ![]() }的前n項和Sn .
}的前n項和Sn .
【答案】
(1)解:設{an}的公比為q,
則a1a2a3=a23=27,∴a2=3,∴a1= ![]() ,a3=3q,
,a3=3q,
∵2a2為3a1和a3的等差中項,
∴4a2=3a1+a3,即12= ![]() +3q,解得q=3或q=1(舍).
+3q,解得q=3或q=1(舍).
∴an=3n﹣1.
(2)解:∵bn=bn﹣1log3an+1=nbn﹣1,
∴ ![]() =n,又b1=1,
=n,又b1=1,
∴bn= ![]()
![]()
![]() …
… ![]() =n!,
=n!,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴Sn=( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)利用等比數列的性質列方程解出公比和a2 , 從而得出通項an;(2)化簡遞推式可得 ![]() =n,使用累乘法得出通項bn , 從而得出{
=n,使用累乘法得出通項bn , 從而得出{ ![]() }的通項,利用裂項法求出Sn .
}的通項,利用裂項法求出Sn .
【考點精析】本題主要考查了數列的前n項和的相關知識點,需要掌握數列{an}的前n項和sn與通項an的關系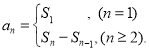 才能正確解答此題.
才能正確解答此題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】(12分)已知函數f(x)對任意的實數m,n都有:f(m+n)=f(m)+f(n)-1,
且當x>0時,有f(x)>1.
(1)求f(0).
(2)求證:f(x)在R上為增函數.
(3)若f(1)=2,且關于x的不等式f(ax-2)+f(x-x2)<3對任意的x∈[1,+∞)恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() ,則下列結論中不正確的是
,則下列結論中不正確的是
A. y與x具有正的線性相關關系
B. 回歸直線過樣本點的中心![]()
C. 若該大學某女生身高增加1 cm,則其體重約增加0.85 kg
D. 若該大學某女生身高為170 cm,則可斷定其體重必為58.79 kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元.在機器使用期間,如果備件不足再購買,則每個500元.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得下面柱狀圖.

記![]() 表示
表示![]() 臺機器在三年使用期內需更換的易損零件數,
臺機器在三年使用期內需更換的易損零件數,![]() 表示
表示![]() 臺機器在購買易損零件上所需的費用(單位:元),
臺機器在購買易損零件上所需的費用(單位:元),![]() 表示購機的同時購買的易損零件數.
表示購機的同時購買的易損零件數.
(1)若![]() ,求
,求![]() 與
與![]() 的函數解析式;
的函數解析式;
(2)若要求 “需更換的易損零件數不大于![]() ”的頻率不小于
”的頻率不小于![]() ,求
,求![]() 的最小值;
的最小值;
(3)假設這![]() 臺機器在購機的同時每臺都購買
臺機器在購機的同時每臺都購買![]() 個易損零件,或每臺都購買
個易損零件,或每臺都購買![]() 個易損零件,分別計算這
個易損零件,分別計算這![]() 臺機器在購買易損零件上所需費用的平均數,以此作為決策依據,購買
臺機器在購買易損零件上所需費用的平均數,以此作為決策依據,購買![]() 臺機器的同時應購買
臺機器的同時應購買![]() 個還是
個還是![]() 個易損零件?
個易損零件?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:x2=2y的焦點為F,過拋物線上一點M作拋物線C的切線l,l交y軸于點N.
(1)判斷△MFN的形狀;
(2)若A,B兩點在拋物線C上,點D(1,1)滿足 ![]() +
+ ![]() =
= ![]() ,若拋物線C上存在異于A,B的點E,使得經過A,B,E三點的圓與拋物線在點E處的有相同的切線,求點E的坐標.
,若拋物線C上存在異于A,B的點E,使得經過A,B,E三點的圓與拋物線在點E處的有相同的切線,求點E的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() .
.
(1)若直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
(2)若![]() 是直線
是直線![]() 上的動點,過
上的動點,過![]() 作圓
作圓![]() 的兩條切線
的兩條切線![]() ,切點為
,切點為![]() ,探究:直線
,探究:直線![]() 是否過定點;
是否過定點;
(3)若![]() 為圓
為圓![]() 的兩條相互垂直的弦,垂足為
的兩條相互垂直的弦,垂足為![]() ,求四邊形
,求四邊形![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的上、下焦點分別為
的上、下焦點分別為![]() ,上焦點
,上焦點![]() 到直線 4x+3y+12=0的距離為3,橢圓C的離心率e=
到直線 4x+3y+12=0的距離為3,橢圓C的離心率e=![]() .
.
(I)若P是橢圓C上任意一點,求![]() 的取值范圍;
的取值范圍;
(II)設過橢圓C的上頂點A的直線![]() 與橢圓交于點B(B不在y軸上),垂直于
與橢圓交于點B(B不在y軸上),垂直于![]() 的直線與
的直線與![]() 交于點M,與
交于點M,與![]() 軸交于點H,若
軸交于點H,若![]() ,且
,且![]() ,求直線
,求直線![]() 的方程.
的方程.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com