
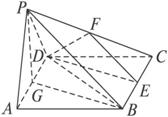
(1)求證:AD⊥PB;
(2)求二面角A-BC-P的大小;
(3)設E為BC邊的中點,F為PC中點,求證:平面DEF⊥平面ABCD.
(1)證明:取AD中點G,連結PG.

∵△PAD為等邊三角形,
∴PG⊥AD.
又由已知平面PAD⊥平面ABCD.
∴PG⊥平面ABCD.
連結BG,BG是PB在平面ABCD上的射影.
由于四邊形ABCD是菱形,∠DAB=60°,
∴△ABD,△BCD均為等邊三角形.
∴BG⊥AD.∴AD⊥PB.
(2)解:∵AD∥BC,∴BG⊥BC,PB⊥BC.
∴∠PBG是二面角ABCP的平面角.
又PG、BG分別是兩個邊長相等的等邊三角形的高.
∴PG=BG.∴∠PBG=45°,
即二面角ABCP的平面角為45°.
(3)證明:∵DE是等邊三角形BCD的中線,
∴BC⊥DE.
∵E、F分別是BC、PC中點,∴EF∥BP.
∴BC⊥EF.∴BC⊥平面DEF.
∴平面DEF⊥平面ABCD.


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:
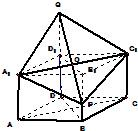 如圖,已知直四棱柱ABCD-A1B1C1D1的底面是邊長為2、∠ADC=120°的菱形,Q是側棱DD1(DD1>
如圖,已知直四棱柱ABCD-A1B1C1D1的底面是邊長為2、∠ADC=120°的菱形,Q是側棱DD1(DD1>
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中數學 來源:《3.2 立體幾何中的向量方法》2013年同步練習3(解析版) 題型:選擇題
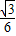
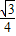
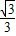

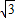
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com