【題目】（本小題滿分12分）某校甲、乙兩個班級各有5名編號為1，2，3，4，5的學生進行投籃訓練，每人投10次，投中的次數統計如下表：
學生 | 1號 | 2號 | 3號 | 4號 | 5號 |
甲班 | 6 | 5 | 7 | 9 | 8 |
乙班 | 4 | 8 | 9 | 7 | 7 |
（1）從統計數據看，甲、乙兩個班哪個班成績更穩定（用數字特征說明）；
（2）在本次訓練中，從兩班中分別任選一個同學，比較兩人的投中次數，求甲班同學投中次數高于乙班同學投中次數的概率．
科目：高中數學 來源： 題型：
【題目】已知函數
，
.
（Ⅰ）求函數
的單調區間；
（Ⅱ）當
時，
，
成立，求
的取值范圍；
（Ⅲ）設曲線
，點
，
為該曲線上不同的兩點.求證：當
時，直線
的斜率大于-1.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人輪流投籃，每人每次投一球．約定甲先投且先投中者獲勝，一直到有人獲勝或每人都已投球3次時投籃結束．設甲每次投籃投中的概率為 
，乙每次投籃投中的概率為 
，且各次投籃互不影響．
（1）求甲獲勝的概率；
（2）求投籃結束時甲的投籃次數ξ的分布列與期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
．
（1）求函數
的最小正周期和對稱軸方程；
（2）若
，求的值域．
【答案】（1）對稱軸為
，最小正周期
；（2）
【解析】
(1)利用正余弦的二倍角公式和輔助角公式將函數解析式進行化簡得到
，由周期公式和對稱軸公式可得答案；(2)由x的范圍得到
，由正弦函數的性質即可得到值域.
（1）
令
，則
的對稱軸為，最小正周期；
（2）當時，，
因為
在
單調遞增，在
單調遞減，
在
取最大值，在
取最小值，
所以
，
所以．
【點睛】
本題考查正弦函數圖像的性質，考查周期性，對稱性，函數值域的求法，考查二倍角公式以及輔助角公式的應用，屬于基礎題.
【題型】解答題
【結束】
21
【題目】已知等比數列
的前
項和為
，公比
，
，
．
（1）求等比數列的通項公式；
（2）設
，求
的前項和
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】把函數y=cos2x+1的圖象上所有點的橫坐標伸長到原來的2倍（縱坐標不變），然后向左平移1個單位長度，再向下平移1個單位長度，得到的圖象是（ ）
A.
B.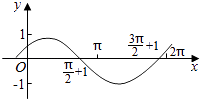
C.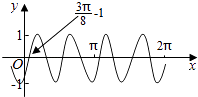
D.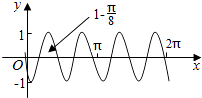
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)對任意x，y∈R，總有f(x)＋f(y)＝f(x＋y)，且當x>0時，f(x)<0，f(1)＝－
.
(1)求證：f(x)是R上的單調減函數．
(2)求f(x)在[－3,3]上的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
