已知函數f(x)的導函數f'(x)是二次函數,且f'(x)=0的兩根為±1.若f(x)的極大值與極小值之和為0,f(-2)=2.
(1)求函數f(x)的解析式;
(2)若函數在開區間(m-9,9-m)上存在最大值與最小值,求實數m的取值范圍.
(3)設函數f(x)=x•g(x),正實數a,b,c滿足ag(b)=bg(c)=cg(a)>0,證明:a=b=c.
【答案】
分析:(1)設f'(x)=a(x+1)(x-1),則可設
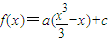
,其中c為常數,利用f(x)的極大值與極小值之和為0,可求c的值,利用f(-2)=2,可求a的值,從而可得函數f(x)的解析式;
(2)確定三次函數在開區間上存在的最大值與最小值必為極值,從而可建立不等式,即可求得實數m的取值范圍;
(3)先判斷a,b,c均小于
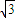
,再利用反證法證明即可.
解答: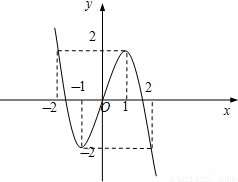
(1)解:設f'(x)=a(x+1)(x-1),則可設
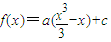
,其中c為常數.
因為f(x)的極大值與極小值之和為0,
所以f(-1)+f(1)=0,即c=0,
由f(-2)=2得a=-3,
所以f(x)=3x-x
3;(5分)
(2)解:由(1)得f(x)=3x-x
3,且f'(x)=-3(x+1)(x-1)
列表:
| x | (-2,-1) | -1 | (-1,1) | 1 | (1,2) |
| y' | - | | + | | - |
| y | ↘ | 極小值-2 | ↗ | 極大值2 | ↘ |
由題意得,三次函數在開區間上存在的最大值與最小值必為極值(如圖),
又f(-2)=2,故f(2)=-2,所以1<9-m≤2,且-2≤m-9<-1,
解得7≤m<8;(10分)
(3)證明:題設等價與a(3-b
2)=b(3-c
2)=c(3-a
2),且a,b,c>0,
所以a,b,c均小于
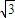
.
假設在a,b,c中有兩個不等,不妨設a≠b,則a>b或a<b.
若a>b,則由a(3-b
2)=b(3-c
2)得3-b
2<3-c
2即b>c,
又由b(3-c
2)=c(3-a
2)得c>a.
于是a>b>c>a,出現矛盾.
同理,若a<b,也必出現出矛盾.
故假設不成立,所以a=b=c.(15分)
點評:本題主要考查利用導數研究三次函數的圖象與性質等基礎知識,考查靈活運用數形結合、化歸與轉化思想進行運算求解、推理論證的綜合能力.

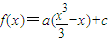 ,其中c為常數,利用f(x)的極大值與極小值之和為0,可求c的值,利用f(-2)=2,可求a的值,從而可得函數f(x)的解析式;
,其中c為常數,利用f(x)的極大值與極小值之和為0,可求c的值,利用f(-2)=2,可求a的值,從而可得函數f(x)的解析式;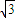 ,再利用反證法證明即可.
,再利用反證法證明即可.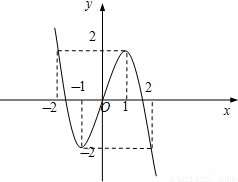 (1)解:設f'(x)=a(x+1)(x-1),則可設
(1)解:設f'(x)=a(x+1)(x-1),則可設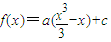 ,其中c為常數.
,其中c為常數.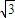 .
.
