Question

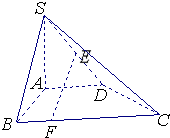
如圖，在四棱錐S-ABCD中，SA⊥底面ABCD，∠BAD=∠ABC=90°，且AB=AD=1，
BC=3，SB與平面ABCD所成的角為45°，E為SD的中點．
（Ⅰ）若F為線段BC上的一點且BF=BC，求證：EF∥平面SAB；
（Ⅱ）求點B到平面SDC的距離；
（Ⅲ）在線段 BC上是否存在一點G，使二面角G-SD-C的大小為arccos？若存在，求出BG的長；若不存在，說明理由．

Answer 1

解：（Ⅰ） 取SA的中點H，連接EH，BH．
由HE∥AD，BF∥AD，且HE=
∴HE∥BF，BF=HE，∴四邊形EFBH為平行四邊形．
∴EF∥BH，BH?平面SAB，EF?平面SAB，
∴EF∥平面SAB．

（Ⅱ）∵SA⊥底面ABCD∴∠SBA是AB與平面ABCD所成的角∴∠SBA=45°SA=AB=1
以A為原點，AB為x軸，圖所示建立直角坐標系，

則B（1，0，0），S（0，0，1），D（0，1，0）C（1，3，0）
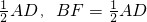
∴=（1，2，0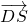）=（0．-1.1）=（0，3，0）
設=（x₁，y₁，z_1）是平SDC的法向量，則
∴∴
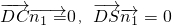
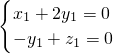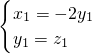
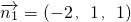取B到平SDC的距離為d==
（Ⅲ） 假設存在，設BG=a，則G（1，a，0）（0＜a＜3）∴
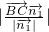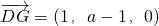
設=（x₂，y₂，z_2）是平面DGS的法向量，則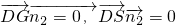
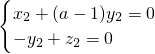∴取
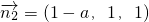
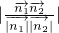由=，得a²=2+（1-a）²
∴，故線段 BC上存在一點G存在G點滿足要求．且
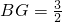
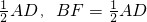分析：（Ⅰ）取SA的中點H，連接EH，BH，根據HE∥AD，BF∥AD，且HE=可得四邊形EFBH為平行四邊形，則EF∥BH，BH?平面SAB，EF?平面SAB，根據線面平行的判定定理可知EF∥平面SAB．
（Ⅱ）求出面SDC的一個法向量，求點B到面SDC的距離實際上是求向量 在面SDC的法向量上的投影的長度．
（Ⅲ）假設存在點G（1，a，0）分別求出GSD面與面CSD的法向量，根據兩法向量的夾角與二面角G-SD-C的大小相等或互補的關系，列出關于a的方程，有解且0＜a＜3則存在，否則不存在．
點評：本題考直線和平面平行的判定，用向量法求點到平面的距離，二面角，考查學生計算能力，邏輯思維能力，方程思想，是中檔題．