
 課堂小作業(yè)系列答案
課堂小作業(yè)系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業(yè)本系列答案
名校作業(yè)本系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
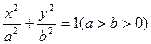 的離心率為
的離心率為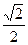 ,其右焦點F是圓
,其右焦點F是圓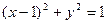 的圓心。
的圓心。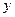 軸于
軸于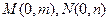 兩點,當
兩點,當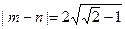 時,求此時點P的坐標。
時,求此時點P的坐標。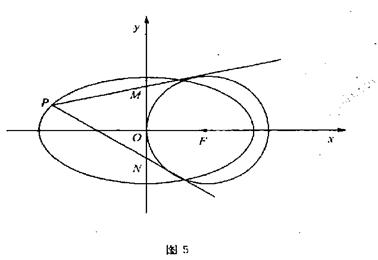
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
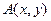 到點
到點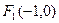 與點
與點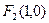 的距離之和為
的距離之和為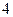
 的軌跡
的軌跡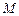 的方程;
的方程;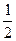 的直線
的直線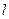 與軌跡
與軌跡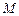 交于
交于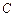 、
、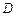 兩點,點
兩點,點 為軌跡
為軌跡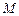 上一點,記直線
上一點,記直線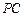 的斜率為
的斜率為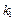 ,直線
,直線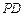 的斜率為
的斜率為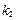 ,試問:
,試問: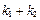 是否為定值?請證明你的結論.
是否為定值?請證明你的結論.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
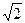 ,BC=1.以AB的中點
,BC=1.以AB的中點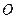 為原點建立如圖8所示的平面直角坐標系
為原點建立如圖8所示的平面直角坐標系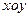 .
.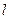 交(Ⅰ)中橢圓于M,N兩點,是否存在直線
交(Ⅰ)中橢圓于M,N兩點,是否存在直線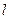 ,使得以弦MN為直徑的圓恰好過原點?若存在,求出直線
,使得以弦MN為直徑的圓恰好過原點?若存在,求出直線 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 :
: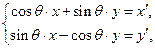 可把平面直角坐標系上的點
可把平面直角坐標系上的點 變換到這一平面上的點
變換到這一平面上的點 .特別地,若曲線
.特別地,若曲線 上一點
上一點 經(jīng)變換公式
經(jīng)變換公式 變換后得到的點
變換后得到的點 與點
與點 重合,則稱點
重合,則稱點 是曲線
是曲線 在變換
在變換 下的不動點.
下的不動點. 的中心為坐標原點,焦點在
的中心為坐標原點,焦點在 軸上,且焦距為
軸上,且焦距為 ,長軸頂點和短軸頂點間的距離為2. 求該橢圓
,長軸頂點和短軸頂點間的距離為2. 求該橢圓 的標準方程. 并求出當
的標準方程. 并求出當 時,其兩個焦點
時,其兩個焦點 、
、 經(jīng)變換公式
經(jīng)變換公式 變換后得到的點
變換后得到的點 和
和 的坐標;
的坐標; 時,求(1)中的橢圓
時,求(1)中的橢圓 在變換
在變換 下的所有不動點的坐標;
下的所有不動點的坐標; :
: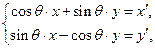 (
( ,
,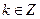 )下的不動點的存在情況和個數(shù).
)下的不動點的存在情況和個數(shù).查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
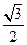 ,過點
,過點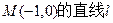 與橢圓交于
與橢圓交于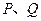 兩點.
兩點.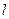 的斜率為1,且
的斜率為1,且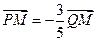 ,求橢圓的標準方程;
,求橢圓的標準方程;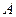 ,直線
,直線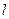 的傾斜角為
的傾斜角為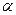 ,問
,問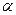 為何值時,
為何值時,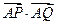 取得最大值,并求出這個最大值.
取得最大值,并求出這個最大值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
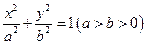 的中心在坐標原點
的中心在坐標原點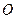 ,一條準線的方程為
,一條準線的方程為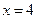 ,過橢圓的左焦點
,過橢圓的左焦點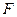 ,且方向向量為
,且方向向量為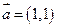 的直線
的直線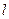 交橢圓于
交橢圓于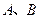 兩點,
兩點,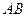 的中點為
的中點為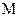
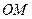 的斜率(用
的斜率(用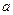 、
、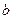 表示);
表示);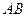 與
與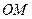 的夾角為
的夾角為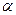 ,當
,當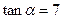 時,求橢圓的方程.
時,求橢圓的方程. 查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
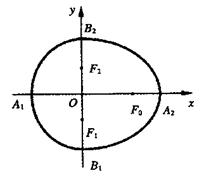
 合成的曲線稱作“果圓”(其中
合成的曲線稱作“果圓”(其中 )。如圖,設點
)。如圖,設點 是相應橢圓的焦點,A1、A2和B1、B2是“果圓”與x,y軸的交點,若△F0F1F2是邊長為1的等邊三角形,則a,b的值分別為 ( )
是相應橢圓的焦點,A1、A2和B1、B2是“果圓”與x,y軸的交點,若△F0F1F2是邊長為1的等邊三角形,則a,b的值分別為 ( )
|
A. | B. | C.5,3 | D.5,4 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com