【題目】將33
33的方格表中毎個格染三種顏色之一,使得每種顏色的格的個數相等.若相鄰兩格的顏色不同,則稱其公共邊為“分隔邊".試求分隔邊條數的最小值。
【答案】56
【解析】
記分隔邊的條數為L。首先,將方格表按圖分成三個區域，分別染成三種顏色，粗線上均為分隔邊。將方格表的行從上至下依次記為
,列從左至右依次記為
。行
中方格出現的顏色數記為
,列
中方格出現的顏色個數記為
。三種顏色分別記為
，對于一種顏色
設
為含有色方格的行數與列數之和。
定義
類似地定義
.計算得到
，再證明
，再證明対任意
均有
最后求出分隔邊條數的最小值.
記分隔邊的條數為L。首先,將方格表按圖分成三個區域，分別染成三種顏色，粗線上均為分隔邊。
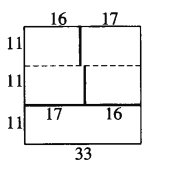
此時,共有56條分隔邊，即L=56。
其次證明:L≥56。
將方格表的行從上至下依次記為,列從左至右依次記為。行中方格出現的顏色數記為,列中方格出現的顏色個數記為。三種顏色分別記為，對于一種顏色設為含有色方格的行數與列數之和。
定義
類似地定義.
所以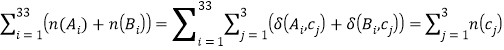
由于染色的格有
個,設含有色方格的行有a個、列有b個,則色的方格一定在這a行和b列的交叉方格中。
從而,
所以
①
由于在行中有種顏色的方格，于是,至少有
條分隔邊。
類似地,在列
中,至少有
條分隔邊。
則
②
③
下面分兩種情形討論。
1.有一行或一列所有方格同色。
不妨設有一行均為
色則方格表的33列中均含有色的方格，又色方格有363個，故至少有11行含有色方格.于是，
④
由式①、③、④得
(2)沒有一行也沒有一列的所有方格同色.
則対任意均有
從而，由式②知;
綜上，分割邊條數的最小值為56.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖，AB為圓O的直徑，點E、F在圓O上，AB
EF，矩形ABCD所在平面和圓O所在平面垂直，已知AB＝2，EF＝1．
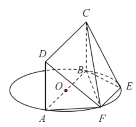
（I）求證：平面DAF⊥平面CBF；
（II）若BC＝1，求四棱錐F－ABCD的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，已知以M點為圓心的圓
及其上一點
.
（1）設圓N與y軸相切，與圓M外切，且圓心在直線
上，求圓N的標準方程；
（2）設平行于OA的直線l與圓M相交于B，C兩點且
，求直線l的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著資本市場的強勢進入，互聯網共享單車“忽如一夜春風來”，遍布了一二線城市的大街小巷.為了解共享單車在
市的使用情況，某調查機構借助網絡進行了問卷調查，并從參與調查的網友中抽取了200人進行抽樣分析，得到表格：（單位：人）
經常使用 | 偶爾或不用 | 合計 | |
30歲及以下 | 70 | 30 | 100 |
30歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
（1）根據以上數據，能否在犯錯誤的概率不超過0.15的前提下認為
市使用共享單車情況與年齡有關？
（2）現從所抽取的30歲以上的網友中利用分層抽樣的方法再抽取5人.
（i）分別求這5人中經常使用、偶爾或不用共享單車的人數；
（ii）從這5人中，再隨機選出2人贈送一件禮品，求選出的2人中至少有1人經常使用共享單車的概率.
參考公式： 
，其中
.
參考數據：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，過函數
的圖象上的兩點
，
作
軸的垂線，垂足分別為
，
，線段
與函數
的圖象交于點
，且
與軸平行．
（1）當
，
，
時，求實數
的值；
（2）當
時，求
的最小值；
（3）已知
，
，若
，
為區間
內任意兩個變量，且
，
求證：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2022年北京冬奧會的申辦成功與“3億人上冰雪”口號的提出，將冰雪這個冷項目迅速炒“熱”．北京某綜合大學計劃在一年級開設冰球課程，為了解學生對冰球運動的興趣，隨機從該校一年級學生中抽取了100人進行調查，其中女生中對冰球運動有興趣的占
，而男生有10人表示對冰球運動沒有興趣額．
（1）完成
列聯表，并回答能否有
的把握認為“對冰球是否有興趣與性別有關”？
（2）若將頻率視為概率，現再從該校一年級全體學生中，采用隨機抽樣的方法每次抽取1名學生，抽取5次，記被抽取的5名學生中對冰球有興趣的人數為
，若每次抽取的結果是相互獨立的，求的分布列，期望和方差．
附表：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】大學生小王自主創業，在鄉下承包了一塊耕地種植某種水果，每季投入2萬元，根據以往的經驗，每季收獲的此種水果能全部售完，且水果的市場價格和這塊地上的產量具有隨機性，互不影響，具體情況如表：
（Ⅰ）設
表示在這塊地種植此水果一季的利潤，求
的分布列及期望；
（Ⅱ）在銷售收入超過5萬元的情況下，利潤超過5萬元的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某位同學進行寒假社會實踐活動，為了對白天平均氣溫與某奶茶店的某種飲料銷量之間的關系進行分析研究，他分別記錄了1月11日至1月15日的白天平均氣溫
與該小賣部的這種飲料銷量
（杯），得到如下數據：
日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均氣溫 | 9 | 10 | 12 | 11 | 8 |
銷量 | 23 | 25 | 30 | 26 | 21 |
（1）若先從這五組數據中抽出2組，求抽出的2組數據恰好是相鄰2天數據的概率；
（2）請根據所給五組數據，求出關于
的線性回歸方程
；
（3）根據（1）中所得的線性回歸方程，若天氣預報1月16日的白天平均氣溫
，請預測該奶茶店這種飲料的銷量.
（參考公式：
，
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
