
已知數列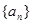 的前n項和
的前n項和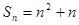 ,數列
,數列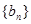 有
有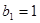 ,
,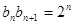
(1)求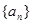 的通項;
的通項;
(2)若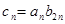 ,求數列
,求數列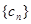 的前n項和
的前n項和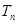 .
.
【解析】第一問中,利用當n=1時,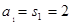
當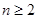 時,
時,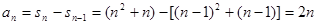
得到通項公式
第二問中,∵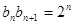 ∴
∴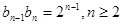 ∴數列
∴數列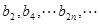 是以2為首項,2為公比的等比數列,利用錯位相減法得到。
是以2為首項,2為公比的等比數列,利用錯位相減法得到。
解:(1)當n=1時,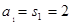 ……………………1分
……………………1分
當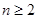 時,
時,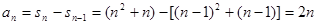 ……4分
……4分
又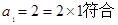
∴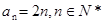 ……………………5分
……………………5分
(2)∵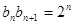 ∴
∴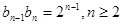
∴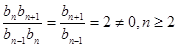 ……………………7分
……………………7分
又∵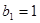 ,
,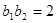 ∴
∴ 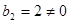
∴數列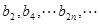 是以2為首項,2為公比的等比數列,
是以2為首項,2為公比的等比數列,
∴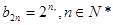 ……………………9分
……………………9分
∴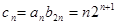
∴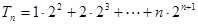 ①
①
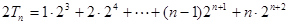 ②
②
①-②得: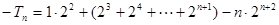
∴
 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| bnbn+1 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年河南省高三第三次大考文科數學 題型:解答題
(本小題滿分12分)已知數列 的前n項和為
的前n項和為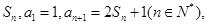 等差數列
等差數列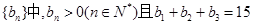 ,又
,又 成等比數列.
成等比數列.
(I)求數列 、
、 的通項公式;
的通項公式;
(II)求數列 的前n項和
的前n項和 .
.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年安徽省皖南八校高三第三次聯考理科數學卷 題型:解答題
已知數列 的前n項和為
的前n項和為
(I)求 的通項公式;
的通項公式;
(II)數列 ,求數列
,求數列 的前n項和
的前n項和 ;
;
(III)若 對一切正整數n恒成立,求實數m的取值范圍。
對一切正整數n恒成立,求實數m的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com