
【題目】已知函數(shù)![]() ,
, ![]() ,
, ![]() 為自然對(duì)數(shù)的底數(shù).
為自然對(duì)數(shù)的底數(shù).
(1)若函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線為
處的切線為![]() ,求
,求![]() 的值;
的值;
(2)當(dāng)![]() 時(shí),若
時(shí),若![]() 在區(qū)間
在區(qū)間![]() 上有兩個(gè)零點(diǎn)
上有兩個(gè)零點(diǎn)![]() ,
,![]() ,試判斷
,試判斷![]() ,
, ![]() ,
, ![]() 的大小關(guān)系.
的大小關(guān)系.
【答案】(1) ![]() (2)
(2) ![]()
【解析】試題分析:(1)第(1)問(wèn),直接利用導(dǎo)數(shù)的幾何意義求出![]() 的值. (2)第(2)問(wèn),先研究函數(shù)g(x)在
的值. (2)第(2)問(wèn),先研究函數(shù)g(x)在![]() 的單調(diào)性得到它的兩個(gè)零點(diǎn)的范圍,
的單調(diào)性得到它的兩個(gè)零點(diǎn)的范圍, ![]() ,
, ![]() ,再作差比較
,再作差比較![]() 和
和![]() 的大小,最后利用函數(shù)的圖像和性質(zhì)比較
的大小,最后利用函數(shù)的圖像和性質(zhì)比較![]() 和
和![]() 的大小.
的大小.
試題解析:
(1)由題意,知![]() ,
, ![]() .
.
因?yàn)?/span>![]() ,所以
,所以![]() ,即
,即![]() .
.
又因?yàn)?/span>![]() ,所以
,所以![]() .
.
(2)由題意,知![]() .
.
因?yàn)?/span>![]() ,
, ![]() ,由
,由![]() ,得
,得![]() 或
或![]() .
.
當(dāng)![]() 時(shí),
時(shí), ![]() ,所以
,所以![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),
時(shí), ![]() ,所以
,所以![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減;
上單調(diào)遞減;
所以![]() 的極小值為
的極小值為![]() .
.
因?yàn)?/span>![]() ,且
,且![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,所以
上單調(diào)遞減,所以![]() .
.
又因?yàn)?/span>![]() ,
, ![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,且
,且![]() ,所以
,所以![]() ,即
,即![]() .
.
當(dāng)![]() 時(shí),
時(shí), ![]() ,
, ![]() .
.
令![]() ,
, ![]() ,則
,則![]() ,設(shè)
,設(shè)![]() ,
,
則![]() 在區(qū)間
在區(qū)間![]() 上恒成立,所以
上恒成立,所以![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() ,
,
所以![]() 在區(qū)間
在區(qū)間![]() 上恒成立,即
上恒成立,即![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,故
上單調(diào)遞增,故![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí), ![]() .
.
又因?yàn)?/span>![]() ,
, ![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,所以
上單調(diào)遞增,所以![]()
所以![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某城市交通部門(mén)為了對(duì)該城市共享單車(chē)加強(qiáng)監(jiān)管,隨機(jī)選取了100人就該城市共享單車(chē)的推行情況進(jìn)行問(wèn)卷調(diào)查,并將問(wèn)卷中的這100人根據(jù)其滿意度評(píng)分值(百分制)按照![]() 分成5組,制成如圖所示頻率分直方圖.
分成5組,制成如圖所示頻率分直方圖.
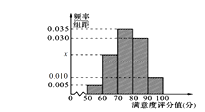
(1)求圖中x的值;
(2)求這組數(shù)據(jù)的平均數(shù)和中位數(shù);
(3)已知滿意度評(píng)分值在![]() 內(nèi)的男生數(shù)與女生數(shù)3:2,若在滿意度評(píng)分值為
內(nèi)的男生數(shù)與女生數(shù)3:2,若在滿意度評(píng)分值為![]() 的人中隨機(jī)抽取2人進(jìn)行座談,求2人均為男生的概率.
的人中隨機(jī)抽取2人進(jìn)行座談,求2人均為男生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() ,判斷函數(shù)
,判斷函數(shù)![]() 的奇偶性,并加以證明;
的奇偶性,并加以證明;
(2)若函數(shù)![]() 在
在![]() 上是增函數(shù),求實(shí)數(shù)
上是增函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若存在實(shí)數(shù)![]() ,使得關(guān)于
,使得關(guān)于![]() 的方程
的方程![]() 有三個(gè)不相等的實(shí)數(shù)根,求實(shí)數(shù)
有三個(gè)不相等的實(shí)數(shù)根,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】判斷下列命題的真假并說(shuō)明理由.
(1)某個(gè)整數(shù)不是偶數(shù),則這個(gè)數(shù)不能被4整除;
(2)若![]() ,且
,且![]() ,則
,則![]() ,且
,且![]() ;
;
(3)合數(shù)一定是偶數(shù);
(4)若![]() ,則
,則![]() ;
;
(5)兩個(gè)三角形兩邊一對(duì)角對(duì)應(yīng)相等,則這兩個(gè)三角形全等;
(6)若實(shí)系數(shù)一元二次方程![]() 滿足
滿足![]() ,那么這個(gè)方程有兩個(gè)不相等的實(shí)根;
,那么這個(gè)方程有兩個(gè)不相等的實(shí)根;
(7)若集合![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,則
,則![]() ;
;
(8)已知集合![]() ,
,![]() ,
,![]() ,如果
,如果![]() ,那么
,那么![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)x=1與x=2是函數(shù)f(x)=aln x+bx2+x的兩個(gè)極值點(diǎn).
(1)試確定常數(shù)a和b的值;
(2)判斷x=1,x=2是函數(shù)f(x)的極大值點(diǎn)還是極小值點(diǎn),并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某鋼管生產(chǎn)車(chē)間生產(chǎn)一批鋼管,質(zhì)檢員從中抽出若干根對(duì)其直徑(單位: ![]() )進(jìn)行測(cè)量,得出這批鋼管的直徑
)進(jìn)行測(cè)量,得出這批鋼管的直徑![]() 服從正態(tài)分布
服從正態(tài)分布![]() .
.
(1)當(dāng)質(zhì)檢員隨機(jī)抽檢時(shí),測(cè)得一根鋼管的直徑為![]() ,他立即要求停止生產(chǎn),檢查設(shè)備,請(qǐng)你根據(jù)所學(xué)知識(shí),判斷該質(zhì)檢員的決定是否有道理,并說(shuō)明判斷的依據(jù);
,他立即要求停止生產(chǎn),檢查設(shè)備,請(qǐng)你根據(jù)所學(xué)知識(shí),判斷該質(zhì)檢員的決定是否有道理,并說(shuō)明判斷的依據(jù);
(2)如果鋼管的直徑![]() 滿足
滿足![]() 為合格品(合格品的概率精確到0.01),現(xiàn)要從60根該種鋼管中任意挑選3根,求次品數(shù)
為合格品(合格品的概率精確到0.01),現(xiàn)要從60根該種鋼管中任意挑選3根,求次品數(shù)![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
(參考數(shù)據(jù):若![]() ,則
,則![]() ;
; ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】分層抽樣是將總體分成互不交叉的層,然后按照一定的比例,從各層獨(dú)立地抽取一定數(shù)量的個(gè)體,組成一個(gè)樣本的抽樣方法;在《九章算術(shù)》第三章“衰分”中有如下問(wèn)題:“今有甲持錢(qián)五百六十,乙持錢(qián)三百五十,丙持錢(qián)一百八十,凡三人俱出關(guān),關(guān)稅百錢(qián).欲以錢(qián)多少衰出之,問(wèn)各幾何?”其譯文為:今有甲持560錢(qián),乙持350錢(qián),丙持180錢(qián),甲、乙、丙三人一起出關(guān),關(guān)稅共100錢(qián),要按照各人帶錢(qián)多少的比例進(jìn)行交稅,問(wèn)三人各應(yīng)付多少稅?則下列說(shuō)法錯(cuò)誤的是( )
A. 甲應(yīng)付![]() 錢(qián) B. 乙應(yīng)付
錢(qián) B. 乙應(yīng)付![]() 錢(qián)
錢(qián)
C. 丙應(yīng)付![]() 錢(qián) D. 三者中甲付的錢(qián)最多,丙付的錢(qián)最少
錢(qián) D. 三者中甲付的錢(qián)最多,丙付的錢(qián)最少
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】執(zhí)行如圖所示的程序框圖,若輸出的結(jié)果為![]() ,則判斷框內(nèi)應(yīng)填入( )
,則判斷框內(nèi)應(yīng)填入( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com