
已知定義在(-∞,—1)∪(1,+∞)上的奇函數滿足:①f(3)=1;②對任意的x>2, 均有f(x)>0,③對任意的x>0,y>0.均有f(x+1)+f(y+1)=f(xy+1)
⑴試求f(2)的值;
⑵證明f(x)在(1,+∞)上單調遞增;
⑶是否存在實數a,使得f(cos2θ+asinθ)<3對任意的θ (0,π)恒成立?若存在,請求出a的范圍;若不存在,請說明理由.
(0,π)恒成立?若存在,請求出a的范圍;若不存在,請說明理由.
1)f(2)=0; 2) 見解析;
3)存在實數a∈(1,9),使得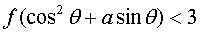 對任意的θ∈(0,π)恒成立.
對任意的θ∈(0,π)恒成立.
【解析】
試題分析:(1)根據對任意的正實數x,y都有均有f(x+1)+f(y+1)=f(xy+1),令x=1,y=1,即可求出f(2)的值;
(2)由于函數沒有具體解析式,要證其在(1,+∞)上為增函數,只能從條件;②對任意的x>2均有f(x)>0和條件③對任意的x>0,y>0,均有f(x+1)+f(y+1)=f(xy+1)入手,取 代入條件③,整理變形后借助于條件②可證出結論.
代入條件③,整理變形后借助于條件②可證出結論.
(3)令x=2,y=2,代入求得f(5),令x=2,y=4,代入求得f(9),
又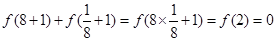 ,可得
,可得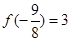 ,根據條件②判斷函數的單調性,根據已知條件把f(cos2θ+asinθ)<3化為cos2θ+asinθ<
,根據條件②判斷函數的單調性,根據已知條件把f(cos2θ+asinθ)<3化為cos2θ+asinθ<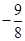 或1<cos2θ+asinθ<9,對任意的θ∈(0,π)恒成立,換元和分離參數即可求得a的范圍..
或1<cos2θ+asinθ<9,對任意的θ∈(0,π)恒成立,換元和分離參數即可求得a的范圍..
1)令X=Y=1得f(2)+f(2)=f(2),∴f(2)=0…………(2分)
2) 任取X1>1,X2>1,X2>X1,則有 從而
從而 ,
,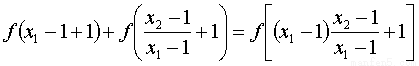
即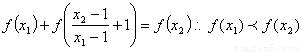
∴f(x)在(1,+∞)上單調遞增……………(8分)
3)因為f(x)為奇函數,且在(1,+∞)上單調遞增,令X=Y=2,得f(5)=f(3)+f(3)=2,再令X=2,Y=4,得f(9)=f(3)+f(5)=3,
由 因為f(x)為奇函數,所以
因為f(x)為奇函數,所以 ,于是f(x)<3的解集為;
,于是f(x)<3的解集為;
(-∞,-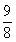 )∪(1,9),于是問題轉化為是否存在實數a,使
)∪(1,9),于是問題轉化為是否存在實數a,使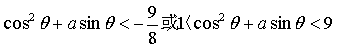 對任意的θ∈(0,π)恒成立,令sinθ=t,則t∈(0,1]于是
對任意的θ∈(0,π)恒成立,令sinθ=t,則t∈(0,1]于是 恒成立等價于
恒成立等價于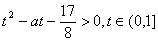 恒成立.即
恒成立.即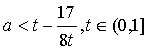 恒成立,當t→0時,
恒成立,當t→0時, ,故不存在實數a使
,故不存在實數a使 對任意的
對任意的
θ∈(0,π)恒成立.
1<cos2θ+asinθ<9恒成立等價于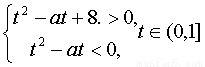 恒成立,得a>1,
恒成立,得a>1,
t2-at+8>0,t∈(0,1]等價于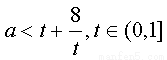 ,
, 在(0,1]單調遞減,于是g(t)min=9,故a<9 于是存在a∈(1,9)使1<cos2θ+asinθ<9 對任意的θ∈(0,π)恒成立.
在(0,1]單調遞減,于是g(t)min=9,故a<9 于是存在a∈(1,9)使1<cos2θ+asinθ<9 對任意的θ∈(0,π)恒成立.
綜上知,存在實數a∈(1,9),使得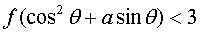 對任意的θ∈(0,π)恒成立.……………………(14分).
對任意的θ∈(0,π)恒成立.……………………(14分).
考點:抽象函數的奇偶性,單調性,函數恒成立問題.
點評:此題是個難題,考查抽象函數及其應用,以及利用函數單調性的定義判斷函數的單調性,并根據函數的單調性解函數值不等式,體現了轉化的思想,在轉化過程中一定注意函數的定義域.解決抽象函數的問題一般應用賦值法.特別是問題(3)的設問形式,增加了題目的難度,綜合性強.


科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| x |
| 1 |
| x |
| f2(x)-2x |
| 2 |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com