
【題目】已知函數(shù)![]() 的圖象在點(diǎn)
的圖象在點(diǎn)![]() 處的切線方程為
處的切線方程為![]() .
.
(Ⅰ)求實數(shù)![]() 、
、![]() 的值;
的值;
(Ⅱ)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值;
上的最大值;
(Ⅲ)曲線![]() 上存在兩點(diǎn)
上存在兩點(diǎn)![]() 、
、![]() ,使得
,使得![]() 是以坐標(biāo)原點(diǎn)
是以坐標(biāo)原點(diǎn)![]() 為直角頂點(diǎn)的直角三角形,且斜邊
為直角頂點(diǎn)的直角三角形,且斜邊![]() 的中點(diǎn)在
的中點(diǎn)在![]() 軸上,求實數(shù)
軸上,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)當(dāng)
;(Ⅱ)當(dāng)![]() 時
時![]() 在[-1,2]上的最大值為2,
在[-1,2]上的最大值為2,
當(dāng)![]() 時
時![]() 在[-1,2]上的最大值為
在[-1,2]上的最大值為![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】試題分析:(1)利用導(dǎo)數(shù)幾何意義: ![]() 可列等量關(guān)系.當(dāng)
可列等量關(guān)系.當(dāng)![]() 時,
時, ![]() 所以
所以![]() ,又
,又![]() 所以
所以![]() 因此
因此 ![]() (2)求分段函數(shù)最值,先分別討論各區(qū)間函數(shù)最值,再比較大小,確定最值.當(dāng)
(2)求分段函數(shù)最值,先分別討論各區(qū)間函數(shù)最值,再比較大小,確定最值.當(dāng)![]() 時,由
時,由![]() 得
得![]() 或
或![]() ,列表分析得
,列表分析得![]() 的最大值為
的最大值為![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() ,需根據(jù)c的值確定函數(shù)最值,當(dāng)
,需根據(jù)c的值確定函數(shù)最值,當(dāng)![]() 時,
時, ![]() 恒成立,
恒成立, ![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() 的最大值為
的最大值為![]() ,比較
,比較![]() 與2的大小得:當(dāng)
與2的大小得:當(dāng)![]() 時,
時, ![]() 在
在![]() 上的最大值為
上的最大值為![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() 在
在![]() 上的最大值為
上的最大值為![]() (3)利用坐標(biāo)探求等量關(guān)系,確定坐標(biāo)所在位置是解題關(guān)鍵.根據(jù)條件
(3)利用坐標(biāo)探求等量關(guān)系,確定坐標(biāo)所在位置是解題關(guān)鍵.根據(jù)條件![]() ,
, ![]() 的橫坐標(biāo)互為相反數(shù),不妨設(shè)
的橫坐標(biāo)互為相反數(shù),不妨設(shè)![]() ,
, ![]() ,
, ![]() .若
.若![]() ,則
,則![]() ,有
,有
![]() ,無解,若
,無解,若![]() ,則
,則![]() .有
.有![]() ,
, ![]() 取值范圍是
取值范圍是![]()
(1)當(dāng)![]() 時,
時, ![]()
所以![]() ,又
,又![]()
所以![]() 因此
因此 ![]()
(2)當(dāng)![]() 時,由
時,由![]() 得
得![]() 或
或![]() ,列表得:
,列表得:
x | -1 | (-1,0) | 0 |
|
|
| 1 |
| - | 0 | + | 0 | - | ||
| 2 | ↘ | ↗ |
| ↘ | 0 |
所以當(dāng)![]() 時,
時, ![]() 的最大值為
的最大值為![]() ,
,
當(dāng)![]() 時,
時, ![]() ,
,
當(dāng)![]() 時,
時, ![]() 恒成立,
恒成立, ![]() ,
,
此時![]() 在
在![]() 上的最大值為
上的最大值為![]() ;
;
當(dāng)![]() 時,
時, ![]() 在
在![]() 上單調(diào)遞增,且
上單調(diào)遞增,且![]() .
.
令![]() ,則
,則![]() ,所以當(dāng)
,所以當(dāng)![]() 時,
時,
![]() 在
在![]() 上的最大值為
上的最大值為![]() ;
;
當(dāng)![]() 時,
時, ![]() 在
在![]() 上的最大值為
上的最大值為![]() .
.
綜上可知,當(dāng)![]() 時,
時, ![]() 在
在![]() 上的最大值為
上的最大值為![]() ;
;
當(dāng)![]() 時,
時, ![]() 在
在![]() 上的最大值為
上的最大值為![]() .
.
⑶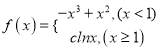 ,根據(jù)條件
,根據(jù)條件![]() ,
, ![]() 的橫坐標(biāo)互為相反數(shù),不妨設(shè)
的橫坐標(biāo)互為相反數(shù),不妨設(shè)![]() ,
, ![]() ,
, ![]() .
.
若![]() ,則
,則![]() ,
,
由![]() 是直角得,
是直角得, ![]() ,即
,即![]() ,
,
即![]() .此時無解;
.此時無解;
若![]() ,則
,則![]() .由于
.由于![]() 的中點(diǎn)在
的中點(diǎn)在![]() 軸上,且
軸上,且![]() ,所以
,所以![]() 點(diǎn)不可能在
點(diǎn)不可能在![]() 軸上,即
軸上,即![]() .同理有
.同理有![]() ,即
,即![]() ,
, ![]() .由于函數(shù)
.由于函數(shù)![]() 的值域是
的值域是![]() ,實數(shù)
,實數(shù)![]() 的取值范圍是
的取值范圍是![]() 即為所求.
即為所求.


 小學(xué)教材全測系列答案
小學(xué)教材全測系列答案 小學(xué)數(shù)學(xué)口算題卡脫口而出系列答案
小學(xué)數(shù)學(xué)口算題卡脫口而出系列答案 優(yōu)秀生應(yīng)用題卡口算天天練系列答案
優(yōu)秀生應(yīng)用題卡口算天天練系列答案 浙江之星課時優(yōu)化作業(yè)系列答案
浙江之星課時優(yōu)化作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),在極坐標(biāo)系(與直角坐標(biāo)系
為參數(shù)),在極坐標(biāo)系(與直角坐標(biāo)系![]() 取相同的長度單位,且以原點(diǎn)
取相同的長度單位,且以原點(diǎn)![]() 為極點(diǎn),以
為極點(diǎn),以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的方程為
的方程為![]() .
.
(1)求圓![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)圓![]() 與直線
與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,若點(diǎn)
,若點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四棱錐P﹣ABCD及其三視圖如下圖所示,E是側(cè)棱PC上的動點(diǎn).
(Ⅰ)求四棱錐P﹣ABCD的體積;
(Ⅱ)不論點(diǎn)E在何位置,是否都有BD⊥AE?試證明你的結(jié)論;
(Ⅲ)若點(diǎn)E為PC的中點(diǎn),求二面角D﹣AE﹣B的大小.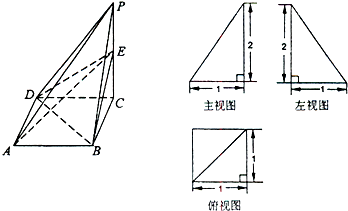
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓F1:(x+1)2+y2=16,定點(diǎn)F2(1,0),A是圓F1上的一動點(diǎn),線段F2A的垂直平分線交半徑F1A于P點(diǎn).
(1)求P點(diǎn)的軌跡C的方程;
(2)四邊形EFGH的四個頂點(diǎn)都在曲線C上,且對角線EG,FH過原點(diǎn)O,
若kEGkFH=-![]() ,求證:四邊形EFGH的面積為定值,并求出此定值.
,求證:四邊形EFGH的面積為定值,并求出此定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的兩個焦點(diǎn)與短軸的一個端點(diǎn)是直角三角形的三個頂點(diǎn),直線
的兩個焦點(diǎn)與短軸的一個端點(diǎn)是直角三角形的三個頂點(diǎn),直線![]() :
: ![]() 與橢圓
與橢圓![]() 有且只有一個公共點(diǎn).
有且只有一個公共點(diǎn).
(Ⅰ)求橢圓![]() 的方程及點(diǎn)
的方程及點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(Ⅱ)設(shè)![]() 是坐標(biāo)原點(diǎn),直線
是坐標(biāo)原點(diǎn),直線![]() 平行于
平行于![]() ,與橢圓
,與橢圓![]() 交于不同的兩點(diǎn)
交于不同的兩點(diǎn)![]() 、
、![]() ,且與直線
,且與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,證明:存在常數(shù)
,證明:存在常數(shù)![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國家“十三五”計劃,提出創(chuàng)新興國,實現(xiàn)中國創(chuàng)新,某市教育局為了提高學(xué)生的創(chuàng)新能力,把行動落到實處,舉辦一次物理、化學(xué)綜合創(chuàng)新技能大賽,某校對其甲、乙、丙、丁四位學(xué)生的物理成績(x)和化學(xué)成績(y)進(jìn)行回歸分析,求得回歸直線方程為y=1.5x﹣35.由于某種原因,成績表(如表所示)中缺失了乙的物理和化學(xué)成績.
甲 | 乙 | 丙 | 丁 | |
物理成績(x) | 75 | m | 80 | 85 |
化學(xué)成績(y) | 80 | n | 85 | 95 |
綜合素質(zhì) | 155 | 160 | 165 | 180 |
(1)請設(shè)法還原乙的物理成績m和化學(xué)成績n;
(2)在全市物理化學(xué)科技創(chuàng)新比賽中,由甲、乙、丙、丁四位學(xué)生組成學(xué)校代表隊參賽.共舉行3場比賽,每場比賽均由賽事主辦方從學(xué)校代表中隨機(jī)抽兩人參賽,每場比賽所抽的選手中,只要有一名選手的綜合素質(zhì)分高于160分,就能為所在學(xué)校贏得一枚榮譽(yù)獎?wù)拢粲洷荣愔汹A得榮譽(yù)獎?wù)碌拿稊?shù)為ξ,試根據(jù)上表所提供數(shù)據(jù),預(yù)測該校所獲獎?wù)聰?shù)ξ的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校課改實行選修走班制,現(xiàn)有甲,乙,丙,丁四位學(xué)生準(zhǔn)備選修物理,化學(xué),生物三個科目.每位學(xué)生只選修一個科目,且選修其中任何一個科目是等可能的.
(1)恰有2人選修物理的概率;
(2)選修科目個數(shù)ξ的分布列及期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)當(dāng)x∈[2,4]時,求該函數(shù)的值域;
(2)若f(x)>mlog2x對于x∈[4,16]恒成立,求m的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com