【題目】若函數
，關于x的方程
有3個不同的實數根，則（ ）
A. b＜﹣2且c＞0B. b＞﹣2且c＜0C. b＝﹣2且c＝0D. b＞﹣2且c＝0
【答案】C
【解析】
令t＝f（x），由關于x的方程
可化為t2+bt+c＝0，設關于t的方程有兩根為t＝t1，t＝t2，由關于x的方程有3個不同的實數根可轉化為函數t＝f（x）的圖象與直線t＝t1，t＝t2的交點個數為3個，作出
的簡圖，利用圖象特征可得：t1＝2，t2＝0，再利用韋達定理列方程得解。
解：令t＝f（x），
則t2+bt+c＝0，
設關于t的方程有兩根為t＝t1，t＝t2，
關于x的方程有3個不同的實數根等價于函數t＝f（x）的圖象與直線t＝t1，t＝t2的交點個數為3個，
作出的簡圖如下：
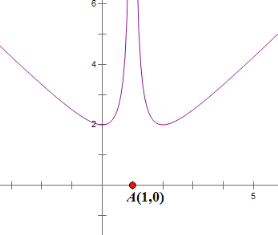
由函數t＝f（x）的圖象與直線t＝t1，t＝t2的位置關系可得：
t1＝2，t2＝0，
由韋達定理可得：
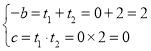，即b＝﹣2，c＝0，
故選：C．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】為了加強環保建設，提高社會效益和經濟效益，某市計劃用若干年時間更換一萬輛燃油型公交車。每更換一輛新車，則淘汰一輛舊車，更換的新車為電力型車和混合動力型車。今年初投入了電力型公交車
輛，混合動力型公交車
輛，計劃以后電力型車每年的投入量比上一年增加
，混合動力型車每年比上一年多投入
輛．設
、
分別為第
年投入的電力型公交車、混合動力型公交車的數量，設
、
分別為年里投入的電力型公交車、混合動力型公交車的總數量。
（1）求
、
，并求年里投入的所有新公交車的總數
；
（2）該市計劃用
年的時間完成全部更換，求的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
為
的導函數，其中
.
（1）當
時，求函數的單調區間；
（2）若方程
有三個互不相同的根0，
，
，其中
.
①是否存在實數
，使得
成立？若存在，求出的值；若不存在，說明理由.
②若對任意的
，不等式
恒成立，求的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某險種的基本保費為
（單位：元），繼續購買該險種的投保人稱為續保人，續保人的本年度的保費與其上年度的出險次數的關聯如下：
上年度出險次數 | 0 | 1 | 2 | 3 | 4 |
|
保費 |
|
|
|
|
|
|
設該險種一續保人一年內出險次數與相應概率如下：
一年內出險次數 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
（Ⅰ）求一續保人本年度的保費高于基本保費的概率；
（Ⅱ）若一續保人本年度的保費高于基本保費，求其保費比基本保費高出
的概率；
（Ⅲ）求續保人本年度的平均保費與基本保費的比值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一段時間內，分5次測得某種商品的價格x(萬元)和需求量y(t)之間的一組數據為：
1 | 2 | 3 | 4 | 5 | |
價格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知
，
(1)畫出散點圖；
(2)求出y對x的線性回歸方程；
(3)如價格定為1.9萬元，預測需求量大約是多少？(精確到0.01 t)．
參考公式：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面直角坐標系xOy中，曲線C：（x﹣1）2+y2=1．直線l經過點P（m，0），且傾斜角為 
．以O為極點，以x軸正半軸為極軸，建立坐標系．
（Ⅰ）寫出曲線C的極坐標方程與直線l的參數方程；
（Ⅱ）若直線l與曲線C相交于A，B兩點，且|PA||PB|=1，求實數m的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
